
���� ���������Բ�ķ��̣�����֪�������Բ�ķ��̼�������Բ�������ʹ�ʽ�õ�������Բ�����������ĵ�ʽ���ⷽ�������a��b��c��ֵ��������Բ���̼��ɣ�
������ֱ�߷���Ϊy-$\frac{1}{2}$=k��x-1����������Բ���̣�����Τ�ﶨ�����е����깫ʽ���ⷽ�̿ɵ�k��ֵ�����ɵõ�����ֱ�ߵķ��̣�
���������E��1��0����ֱ�߷���Ϊy=k��x-1����������Բ���̣�����Τ�ﶨ��������|EP|=2|EQ|���ɵ�$\overrightarrow{EP}$=-2$\overrightarrow{EQ}$�����������������ʾ���ⷽ�̼��ɵõ�k��ֵ�������õ�����ֱ�ߵķ��̣�
���������ֱ�ߵķ��̣���ֱ�߷�������Բ������������ȥx�õ�����y�Ķ��η��̣�����Τ�ﶨ���õ������������������Ĺ�ϵ����ֱ��OP��PQ��OQ��б���������ʾ������֪����б�ʳɵȱ����У��г����̣���Τ�ﶨ���õ��ĵ�ʽ���룬���k��ֵ�������б�ʽ����0�õ�m�ķ�Χ������OPQ�����m��ʾ���������ķ�Χ��
��� �⣺���������������Բ����Ϊ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����
����e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$��a2-b2=c2��$\frac{2}{{a}^{2}}$+$\frac{1}{2{b}^{2}}$=1��
���a=2��b=1��
����Բ����Ϊ$\frac{{x}^{2}}{4}$+y2=1��
����D��1��$\frac{1}{2}$��������Բ���̣��ɵ�$\frac{1}{4}$+$\frac{1}{4}$��1��D����Բ�ڣ�
��ֱ�߷���Ϊy-$\frac{1}{2}$=k��x-1������Ϊy=kx+$\frac{1}{2}$-k��
������Բ���̣��ɵã�1+4k2��x2+8k��$\frac{1}{2}$-k��x+4��$\frac{1}{2}$-k��2-4=0��
��P��x1��y1����Q��x2��y2������x1+x2=$\frac{8{k}^{2}-4k}{1+4{k}^{2}}$��
��|DP|=|DQ|���ɵ�DΪPQ���е㣬
��$\frac{4{k}^{2}-2k}{1+4{k}^{2}}$=1�����k=-$\frac{1}{2}$��
����ֱ�ߵķ���Ϊy=-$\frac{1}{2}$x+1��
���������E��1��0����ֱ�߷���Ϊy=k��x-1����������Բ���̣��ɵ�
��1+4k2��x2-8k2x+4k2-4=0��
��P��x1��y1����Q��x2��y2������x1+x2=$\frac{8{k}^{2}}{1+4{k}^{2}}$��x1x2=$\frac{4{k}^{2}-4}{1+4{k}^{2}}$����
��|EP|=2|EQ|���ɵ�$\overrightarrow{EP}$=-2$\overrightarrow{EQ}$��
��x1-1=-2��x2-1��������x1=-2x2+3����
�ɢ٢ڿɵ�x2=$\frac{3+4{k}^{2}}{1+4{k}^{2}}$��x1=$\frac{4{k}^{2}-3}{1+4{k}^{2}}$��
����$\frac{16{k}^{4}-9}{��1+4{k}^{2}��^{2}}$=$\frac{4{k}^{2}-4}{1+4{k}^{2}}$�����k=��$\frac{\sqrt{15}}{6}$��
����ֱ�ߵķ���Ϊy=��$\frac{\sqrt{15}}{6}$��x-1����
�������������֪��ֱ��l��б�ʴ����Ҳ�Ϊ0��
�ʿ���ֱ��l�ķ���Ϊy=kx+m��m��0����P��x1��y1����Q��x2��y2����
��$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+4{y}^{2}=4}\end{array}\right.$����ȥy��
��1+4k2��x2+8kmx+4��m2-1��=0��
���=64k2b2-16��1+4k2b2����b2-1��=16��4k2-m2+1����0��
��x1+x2=-$\frac{8km}{1+4{k}^{2}}$��x1•x2=$\frac{4��{m}^{2}-1��}{1+4{k}^{2}}$��
��y1y2=��kx1+m����kx2+m��=k2x1x2+km��x1+x2��+m2��
��Ϊֱ��OP��PQ��OQ��б�����γɵȱ����У�
����$\frac{{y}_{1}}{{x}_{1}}$•$\frac{{y}_{2}}{{x}_{2}}$=$\frac{{k}^{2}{x}_{1}{x}_{2}+km��{x}_{1}+{x}_{2}��+{m}^{2}}{{x}_{1}{x}_{2}}$=k2��
��-$\frac{8{k}^{2}{m}^{2}}{1+4{k}^{2}}$+m2=0����m��0��
����k2=$\frac{1}{4}$����k=��$\frac{1}{2}$��
����ֱ��OP��OQ��б�ʴ��ڣ��ҡ���0����
0��m2��2��m2��1��
��O��ֱ��l�ľ���d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$��
��S��OPQ=$\frac{1}{2}$d|PQ|=$\frac{1}{2}$|x1-x2|•|m|=$\frac{1}{2}$|m|•$\sqrt{\frac{64{k}^{2}{m}^{2}}{��1+4{k}^{2}��^{2}}-\frac{16��{m}^{2}-1��}{1+4{k}^{2}}}$
=$\sqrt{{m}^{2}��2-{m}^{2}��}$��$\frac{{m}^{2}+2-{m}^{2}}{2}$=1��
����S��OPQ��ȡֵ��ΧΪ��0��1����
���� ���⿼����Բ���̵���ע��������Բ�������ʺ͵�������Բ���̣�����ֱ����Բ���ߵ�λ�ù�ϵ���⣬һ�����ֱ�߷��̣���ֱ�߷�����Բ���߷�����������ȥһ��δ֪�����õ�����һ��δ֪���Ķ��η��̣�����Τ�ﶨ����ע�������������ߺ͵㵽ֱ�ߵľ��빫ʽ�ͻ�������ʽ��ע����ֱ�߷���ʱ��һ��Ҫ����ֱ�ߵ�б���Ƿ���ڣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | p��q | B�� | ���Vp���ģ��Vq�� | C�� | ���Vp����q | D�� | p��q |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | $\frac{1}{2}$ | D�� | -$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
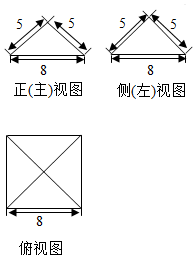 һ�������������ͼ����ߴ���ͼ��ʾ����ü�����ı����Ϊ��������
һ�������������ͼ����ߴ���ͼ��ʾ����ü�����ı����Ϊ��������| A�� | 48 | B�� | 80 | C�� | 112 | D�� | 144 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com