
分析 构造思想,sinβ=sin[(α+β)-α],再利用和与差公式直接求解即可.
解答 解:α∈(0,$\frac{π}{2}$),sinα=$\frac{3}{5}$
可得:cosα=$\frac{4}{5}$
∵β∈($\frac{π}{2}$,π),
∴α+β∈($\frac{π}{2},\frac{3π}{2}$),
又sin(α+β)=-$\frac{4}{5}$<0,
∴cos(α+β)=-$\frac{3}{5}$
则sinβ=sin[(α+β)-α]=sin(α+β)cosα-cos(α+β)sinα=$-\frac{7}{25}$.
故答案为$-\frac{7}{25}$
点评 本题考查了构造思想,和与差公式的运用和计算能力.属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
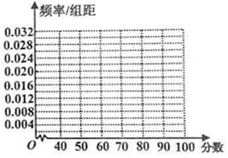 学校从参加高三年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),得到如下数学成绩的频率分布表:
学校从参加高三年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),得到如下数学成绩的频率分布表:| 分组 | 频数 | 频率 |
| [40,50) | 2 | |
| [50,60) | 3 | |
| [60,70) | 0.28 | |
| [70,80) | 15 | |
| [80,90) | 12 | |
| [90,100] | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π2 | B. | 4π2 | C. | π | D. | 2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
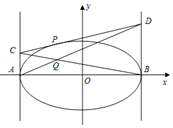 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{3}$,联接椭圆四个顶点的四边形面积为2$\sqrt{6}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{3}$,联接椭圆四个顶点的四边形面积为2$\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com