
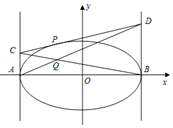
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{3}$,联接椭圆四个顶点的四边形面积为2$\sqrt{6}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{3}$,联接椭圆四个顶点的四边形面积为2$\sqrt{6}$.分析 (1)由椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{3}$,联接椭圆四个顶点的四边形面积为2$\sqrt{6}$,列出方程组,求出a,b,由此能求出椭圆C的方程.
(2)设切线方程为y=kx+m,与椭圆联立消元得(2+3k2)x2+6kmx+3m2-6=0,由此利用根的判别式、韦达定理、直线方程,组合已知条件能求出存在λ=1,使xP=λxQ恒成立.
解答 解:(1)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{3}$,联接椭圆四个顶点的四边形面积为2$\sqrt{6}$,
∴$\left\{\begin{array}{l}{e=\frac{c}{a}=\frac{\sqrt{3}}{3}}\\{2ab=2\sqrt{6}}\end{array}\right.$,解得a=$\sqrt{3}$,b=$\sqrt{2}$,
故椭圆C的方程为$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$.…(4分)
(2)设切线方程为y=kx+m,
与椭圆联立消元得(2+3k2)x2+6kmx+3m2-6=0,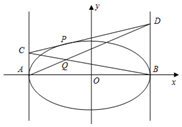
∵切线与椭圆相切,∴△=36k2m2-4(2+3k2)(3m2-6)=0,
化简得m2=2+3k2,…(6分)且${x}_{P}=-\frac{6km}{2(2+3{k}^{2})}$=-$\frac{3k}{m}$,…(8分)
又直线AD方程为y=$\frac{m+\sqrt{3}k}{2\sqrt{3}}$(x+$\sqrt{3}$),
直线BC方程为y=$\frac{m-\sqrt{3}k}{2-\sqrt{3}}$(x-$\sqrt{3}$),
解得xQ=-$\frac{3k}{m}$,…(10分)
∴存在λ=1,使xP=λxQ恒成立.…(12分)
点评 本题考查椭圆方程的求法,考查满足条件的实数值的求法,考查推理论证能力、运算求解能力,考查化归与转化思想,函数与方程思想,是中档题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小正周期为π的偶函数 | B. | 最小正周期为π的奇函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的偶函数 | D. | 最小正周期为$\frac{π}{2}$的奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
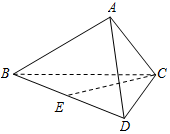 如图,在四面体ABCD中,平面ABC⊥平面BCD,DC⊥BC,$AB=\sqrt{3}$,BC=2,AC=1.
如图,在四面体ABCD中,平面ABC⊥平面BCD,DC⊥BC,$AB=\sqrt{3}$,BC=2,AC=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x±y=0 | B. | x±2y=0 | C. | 3x±4y=0 | D. | 4x±3y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com