
分析 (1)随机变量X的所有可能取值为110,50,30,-30,计算对应的概率值,写出X的分布列,计算数学期望;
(2)设某人玩5次游戏B的过程中,出现音乐n次,列不等式求出n的值,再计算“某人玩5次游戏B能兑换奖品”的概率值.
解答 解:(1)随机变量X的所有可能取值为110,50,30,-30,分别对应以下四种情况:
①玩游戏A,绿灯闪亮,且玩游戏B,出现音乐;
②玩游戏A,绿灯不闪亮,且玩游戏B,出现音乐;
③玩游戏A,绿灯闪亮,且玩游戏B,没有出现音乐;
④玩游戏A,绿灯不闪亮,且玩游戏B,没有出现音乐,
所以$P(X=110)=\frac{1}{2}×\frac{2}{5}=\frac{1}{5}$,
$P(X=50)=(1-\frac{1}{2})×\frac{2}{5}=\frac{1}{5}$,
$P(X=30)=\frac{1}{2}×(1-\frac{2}{5})=\frac{3}{10}$,
$P(X=-30)=(1-\frac{1}{2})×(1-\frac{2}{5})=\frac{3}{10}$,
即X的分布列为:
| X | 110 | 50 | 30 | -30 |
| P | $\frac{1}{5}$ | $\frac{1}{5}$ | $\frac{3}{10}$ | $\frac{3}{10}$ |
点评 本题考查了离散型随机变量分布列与数学期望的应用问题,是基础题.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
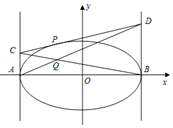 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{3}$,联接椭圆四个顶点的四边形面积为2$\sqrt{6}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{3}$,联接椭圆四个顶点的四边形面积为2$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{10}$ | B. | $\frac{3}{10}$ | C. | $-\frac{3}{10}$ | D. | $-\frac{9}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com