练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．函数y=2sin2（x+$\frac{3π}{2}$）-1是（　　）
    A．最小正周期为π的偶函数B．最小正周期为π的奇函数
    C．最小正周期为$\frac{π}{2}$的偶函数D．最小正周期为$\frac{π}{2}$的奇函数

    分析 将函数y化简，根据三角函数的性质可得答案．

    解答 解：函数y=2sin2（x+$\frac{3π}{2}$）-1，
    化简可得y=-cos（2x+3π）=cos2x．
    ∴函数y是最小正周期T=$\frac{2π}{2}$=π的偶函数．
    故选A．

    点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用，利用三角函数公式将函数进行化简是解决本题的关键．属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    13．学校从参加高三年级期中考试的学生中抽出50名学生，并统计了他们的数学成绩（成绩均为整数且满分为100分），得到如下数学成绩的频率分布表：
    分组频数频率
    [40，50）2
    [50，60）3
    [60，70）0.28
    [70，80）15
    [80，90）12
    [90，100]4
    （Ⅰ）请在答题卡上完成频率分布表和作出频率分布直方图；
    （Ⅱ）用样本估计总体，若高三年级共有2000人，估计成绩不及格（60分以下）的人数；
    （Ⅲ）为了帮助成绩差的学生提高数学成绩，现从成绩[90，100]的学生中选两位同学，共同帮助成绩在[40，50）中的某一位同学，即成立帮扶学习小组，样本中已知甲同学的成绩为42分，乙同学的成绩为95分，求甲、乙两同学恰好被安排在同一小组的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．数列{an}对于确定的正整数m，若存在正整数n使得am+n=am+an成立，则称数列{an}为“m阶可分拆数列”．
    （1）设{an}是首项为2，公差为2的等差数列，证明{an}为“3阶可分拆数列”；
    （2）设数列{an}的前n项和为${S_n}={2^n}-a$（a＞0），若数列{an}为“1阶可分拆数列”，求实数a的值；
    （3）设${a_n}={2^n}+{n^2}+12$，试探求是否存在m使得若数列{an}为“m阶可分拆数列”．若存在，请求出所有m，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．设i为虚数单位，若$z=\frac{a-i}{1+i}（a∈{R}）$是纯虚数，则a的值是（　　）
    A．-1B．0C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．甲，乙两台机床同时生产一种零件，其质量按测试指标划分：指标大于或等于95为正品，小于95为次品，现随机抽取这两台车床生产的零件各100件进行检测，检测结果统计如下：
    测试指标[85，90）[90，95）[95，100）[100，105）[105，110）
    机床甲81240328
    机床乙71840296
    （1）试分别估计甲机床、乙机床生产的零件为正品的概率；
    （2）甲机床生产一件零件，若是正品可盈利160元，次品则亏损20元；乙机床生产一件零件，若是正品可盈利200元，次品则亏损40元，在（1）的前提下，现需生产这种零件2件，以获得利润的期望值为决策依据，应该如何安排生产最佳？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．若向量$\overrightarrow{m}$=（2，1），$\overrightarrow{n}$=（-3，2λ），且（2$\overrightarrow{m}$-$\overrightarrow{n}$）∥（$\overrightarrow{m}$+3$\overrightarrow{n}$），则实数λ=-$\frac{3}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．设函数f（x）=|2x-1|+3x-4，记不等式f（x）＜-3的解集为M．
    （Ⅰ）求M；
    （Ⅱ）当x∈M时，证明：x[f（x）]2-x2|f（x）|＜0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

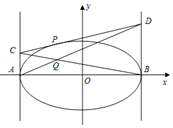    6．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{3}$，联接椭圆四个顶点的四边形面积为2$\sqrt{6}$．
    （1）求椭圆C的方程；
    （2）A、B是椭圆的左右顶点，P（xP，yP）是椭圆上任意一点，椭圆在P点处的切线与过A、B且与x轴垂直的直线分别交于C、D两点，直线AD、BC交于Q（xQ，yQ），是否存在实数λ，使xP=λxQ恒成立，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．点A，B，C，D在同一个球的球面上，AB=BC=$\sqrt{6}$，∠ABC=90°，若四面体ABCD体积的最大值为3，则这个球的表面积为（　　）
    A．2πB．4πC．8πD．16π

    查看答案和解析>>

    同步练习册答案