
| A. | 2π | B. | 4π | C. | 8π | D. | 16π |
分析 根据几何体的特征,判定外接球的球心,求出球的半径,即可求出球的表面积
解答 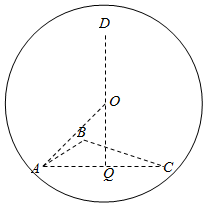 解:根据题意知,直角三角形△ABC的面积为3.其所在球的小圆的圆心在斜边AC的中点上,设小圆的圆心为Q,
解:根据题意知,直角三角形△ABC的面积为3.其所在球的小圆的圆心在斜边AC的中点上,设小圆的圆心为Q,
若四面体ABCD的体积的最大值,由于底面积S△ABC不变,高最大时体积最大,
所以,DQ与面ABC垂直时体积最大,最大值为为$\frac{1}{3}$S△ABC×DQ=3,
即$\frac{1}{3}$×3×DQ=3,∴DQ=3,如图.设球心为O,半径为R,则在直角△AQO中,
OA2=AQ2+OQ2,即R2=($\sqrt{3}$)2+(3-R)2,∴R=2,
则这个球的表面积为:S=4π×22=16π.
故选:D.
点评 本题考查的知识点是球内接多面体,球的表面积,其中分析出何时四面体ABCD的体积的最大值,是解答的关键,考查等价转化思想思想,是中档题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 最小正周期为π的偶函数 | B. | 最小正周期为π的奇函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的偶函数 | D. | 最小正周期为$\frac{π}{2}$的奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
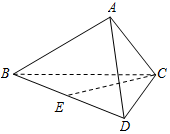 如图,在四面体ABCD中,平面ABC⊥平面BCD,DC⊥BC,$AB=\sqrt{3}$,BC=2,AC=1.
如图,在四面体ABCD中,平面ABC⊥平面BCD,DC⊥BC,$AB=\sqrt{3}$,BC=2,AC=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x±y=0 | B. | x±2y=0 | C. | 3x±4y=0 | D. | 4x±3y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6≤k≤2 | B. | -6≤k≤-2 | C. | -2≤k≤6 | D. | 2≤k≤6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
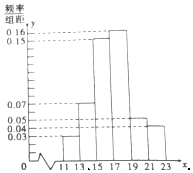 一企业从某生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到的频率分布直方图如图.
一企业从某生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到的频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com