
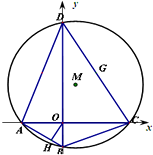
 ��ͼ����ƽ��ֱ������ϵ�У�����Ϊx2+y2+DX+Ey+F=0��ԲM���ڽ��ı���ABCD�ĶԽ���AC��BD���ഹֱ����AC��BD�ֱ���x���y���ϣ�
��ͼ����ƽ��ֱ������ϵ�У�����Ϊx2+y2+DX+Ey+F=0��ԲM���ڽ��ı���ABCD�ĶԽ���AC��BD���ഹֱ����AC��BD�ֱ���x���y���ϣ����� ��1��������֪�Խ����ഹֱ���ı���ABCD���$S=\frac{{|{AC}|•|{BD}|}}{2}$������MA����M��0��3�����ɴ�����������
��2�����ı����ĸ����������ֱ�ΪA��a��0����B��0��b����C��c��0����D��d��0�������G������Ϊ$��{\frac{c}{2}��\frac{d}{2}}��$��ʹG��O��H���ߣ�ֻ��֤$\overrightarrow{AB}•\overrightarrow{OG}=0$���ɣ��ɴ���֤��G��O��H�ض����㹲�ߣ�
��� �⣺��1��������֪�Խ����ഹֱ���ı���ABCD���$S=\frac{{|{AC}|•|{BD}|}}{2}$��
��S=40��AC=8����BD=10������2�֣�
�֡�$\overrightarrow{AB}•\overrightarrow{AD}=0$�����AΪֱ�ǣ����ı�����ԲM���ڽ��ı��Σ���BD=2r=10��r=5��
����MA�����MO=3����M��0��3����
��ԲM�ķ���Ϊx2+��y-3��2=25������6�֣�
��x=0��y=8��y=-2����B��0��8����D��0��-2������8�֣�
֤������2�����ı����ĸ����������ֱ�ΪA��a��0����B��0��b����C��c��0����D��d��0����
���G������Ϊ$��{\frac{c}{2}��\frac{d}{2}}��$����$\overrightarrow{OG}=��{\frac{c}{2}��\frac{d}{2}}��$����12�֣�
��$\overrightarrow{AB}=��{-a��b}��$����AB��OH����ʹG��O��H���ߣ�ֻ��֤$\overrightarrow{AB}•\overrightarrow{OG}=0$����
��$\overrightarrow{AB}•\overrightarrow{OG}=\frac{bd-ac}{2}$���Ҷ���ԲM��һ�㷽��x2+y2+DX+Ey+F=0��
��y=0ʱ���ɵ�x2+DX+F=0�����з��̵������ֱ�Ϊ��A�͵�C�ĺ����꣬
������xAxC=ac=F��
ͬ������x=0ʱ���ɵ�y2+Ey+F=0�����з��̵������ֱ�Ϊ��B�͵�D�������꣬
������yByD=bd=F�����ԣ�$\overrightarrow{AB}•\overrightarrow{OG}=\frac{bd-ac}{2}=0$����AB��OG��
��G��O��H�ض����㹲�� ����16�֣�
���� ���⿼�鷽�̵����������㹲�ߵ�֤�������е��⣬����ʱҪ�������⣬ע��Բ�����ʵĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{11}{2}$ | B�� | $\frac{7}{2}$ | C�� | 7 | D�� | -5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | p��q�� | B�� | p��q�� | C�� | p��q���� | D�� | p��q�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ͼ�����ԭ��Գƣ���R��Ϊ������ | B�� | ͼ�����y��Գƣ���R��Ϊ������ | ||
| C�� | ͼ�����ԭ��Գƣ���R��Ϊ������ | D�� | ͼ�����y��Գƣ���R��Ϊ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com