
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 由已知条件利用对数的运算法则和函数的性质求出f(x)+f(-x)=1,由此能求出f(lg2)+f(lg$\frac{1}{2}$)的值.
解答 解:∵f(x)=lg($\sqrt{1+4{x}^{2}}$-2x)+$\frac{1}{2}$,
∴f(x)+f(-x)=[lg($\sqrt{1+4{x}^{2}}$-2x)+$\frac{1}{2}$]+[lg($\sqrt{1+4{x}^{2}}$+2x)+$\frac{1}{2}$]
=[lg($\sqrt{1+4{x}^{2}}$-2x)+lg($\sqrt{1+4{x}^{2}}$+2x)]+1
=lg[(1+4x2-4x2)+1
=lg1+1
=1,
∴f(lg2)+f(lg$\frac{1}{2}$)=f(lg2)+f(-lg2)=1.
故选:C.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意对数运算法则和函数性质的合理运用.


科目:高中数学 来源: 题型:选择题
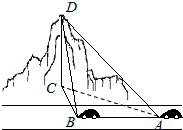 如图,有一辆汽车在一条水平的公路上向正西行驶,汽车在A点测得公路北侧山顶D的仰角为30°,汽车行驶300m后到达B点测得山顶D恰好在正北方,且仰角为45°,则山的高度CD为( )
如图,有一辆汽车在一条水平的公路上向正西行驶,汽车在A点测得公路北侧山顶D的仰角为30°,汽车行驶300m后到达B点测得山顶D恰好在正北方,且仰角为45°,则山的高度CD为( )| A. | 150$\sqrt{2}$ | B. | 150$\sqrt{3}$ | C. | 300$\sqrt{2}$ | D. | 300$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{\sqrt{2}}{2}$] | B. | (0,$\frac{3}{4}$] | C. | [$\frac{\sqrt{2}}{2}$,$\frac{3}{4}$] | D. | ($\frac{3}{4}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
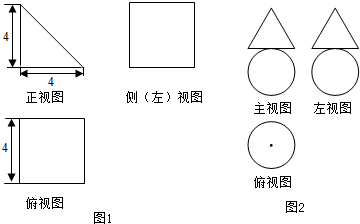
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com