
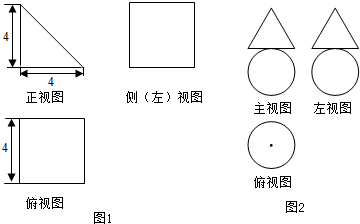
分析 (1)由已知中的三视图,可得该几何体是一个以正视图为底面的三棱柱,代入柱休表面积公式,可得答案;
(2)由已知中的三视图,可得该几何体是一个圆锥和一个球的组合体,结合球和圆锥的体积公式,可得答案.
解答 解:(1)由已知中的三视图,可得该几何体是一个以正视图为底面的三棱柱,
故其表面积S=2×$\frac{1}{2}$×4×4+(4+4+$\sqrt{{4}^{2}+{4}^{2}}$)×4=48+16$\sqrt{2}$;
(2)由已知中的三视图,可得该几何体是一个圆锥和一个球的组合体,
圆锥底面和球的直径均为2,故半径均为1,圆锥的高为$\sqrt{3}$,
故组合体的体积V=$\frac{4}{3}π$+$\frac{1}{3}π×\sqrt{3}$=$\frac{4+\sqrt{3}}{3}π$
点评 本题考查的知识点是由三视图求体积和表面积,根据三视图判断出几何体的形状是解答的关键.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
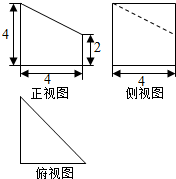
| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | 16 | D. | $\frac{80}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=-2cos x | B. | f(x)=2cos x | ||
| C. | f(x)=$\frac{\sqrt{2}}{2}$sin 2x | D. | f(x)=$\frac{\sqrt{2}}{2}$(sin 2x+cos 2x) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
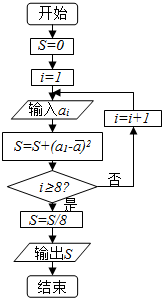 对一名学生数学成绩统计了8次,第i次统计得到的数据为ai,具体如下表所示:
对一名学生数学成绩统计了8次,第i次统计得到的数据为ai,具体如下表所示:| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ai | 100 | 101 | 103 | 103 | 104 | 106 | 107 | 108 |
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com