Question

【题目】为调查宜昌一中高二年级男生的身高状况，现从宜昌一中高二年级中随机抽取100名男生作为样本，下图是样本的身高频率分布直方图(身高单位：cm).

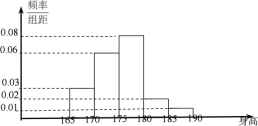
（1）用样本频率估计高二男生身高在180cm及以上概率，并根据图中数据估计宜昌一中高二男生的平均身高；

（2）在该样本中，求身高在180cm及以上的同学人数，利用分层抽样的方法再从身高在180cm及以上的两组同学（180~185，185~190）中选出3名同学，应该如何选取；

（3）在该样本中，从身高在180cm及以上的同学中随机挑选3人，这3人的身高都在185cm及以上的概率有多大？

Answer 1

【答案】（1），；（2）在180cm至185cm一组内随机选2人、在185cm至190cm一组内随机选1人；（3）

【解析】

（1）根据图中数据直接计算即可

（2）样本中，180cm至185cm一组频率为0.1，其人数为人，185cm至190cm一组频率为0.05，其人数为人，然后即可算出答案

（3）分别算出总的个数和这3人的身高都在185cm及以上的个数，然后相比即可得出答案

（1）样本中180cm及以上的频率为，

所以高二男生身高在180cm及以上的概率为；

高二男生平均身高为cm.

（2）样本中，180cm至185cm一组频率为0.1，其人数为人，

185cm至190cm一组频率为0.05，其人数为人，

两组合计共15人，采用分层抽样选3人，应在180cm至185cm一组内随机选2人、

在185cm至190cm一组内随机选1人；

（3）样本中身高在180cm及以上共15人，

从中随机抽选3人的所有选法为种，

身高在185cm及以上的人数为5，

从中随机抽选3人的所有选法为种，

故身高都在185cm及以上的概率为.