
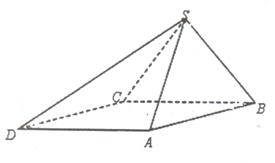
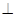 底面ABCD.已知
底面ABCD.已知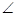 ABC=45o,AB=2,BC=2
ABC=45o,AB=2,BC=2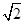 ,SA=SB=
,SA=SB=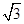 .
.
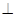 BC;
BC;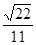 .
.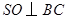 ,由侧面
,由侧面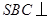 底面
底面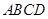 ,得
,得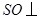 平面
平面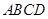 .证明线线垂直,有两个思路,一是通过线面垂直转化,二是利用空间向量计算.本题考虑到第二小题,采取空间向量方法. 利用空间向量以算代证,关键正确表示各点及对应向量的坐标,利用空间向量数量积进行论证.(2)利用空间向量求线面角,关键正确求出平面的一个法向量,利用两向量夹角的余弦值的绝对值等于线面角的正弦值的等量关系进行求解.
.证明线线垂直,有两个思路,一是通过线面垂直转化,二是利用空间向量计算.本题考虑到第二小题,采取空间向量方法. 利用空间向量以算代证,关键正确表示各点及对应向量的坐标,利用空间向量数量积进行论证.(2)利用空间向量求线面角,关键正确求出平面的一个法向量,利用两向量夹角的余弦值的绝对值等于线面角的正弦值的等量关系进行求解.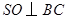 ,垂足为
,垂足为 ,连结
,连结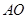 ,
,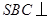 底面
底面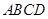 ,
,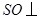 平面
平面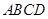 ..2
..2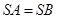 ,所以
,所以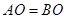 3
3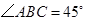 ,
,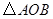 为等腰直角三角形,
为等腰直角三角形, 4
4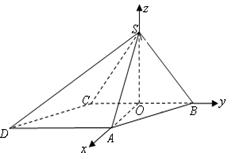
 为坐标原点,
为坐标原点,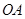 为
为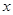 轴正向,建立直角坐标系
轴正向,建立直角坐标系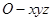 .
.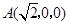 ,
,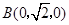 ,
,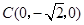 ,
,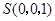 ,
,  6
6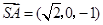 ,
, ,
, ,所以
,所以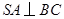 8
8 为平面SAB的法向量
为平面SAB的法向量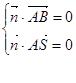 得
得  所以
所以 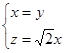
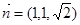 10
10 12
12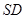 与平面
与平面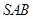 所成的角与
所成的角与 与
与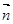 所成的角互余.
所成的角互余.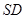 与平面
与平面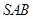 所成的角正弦值为
所成的角正弦值为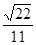 13
13

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源:不详 题型:解答题
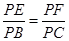 =λ.
=λ.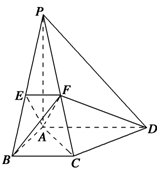
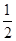 时,求异面直线BF与CD所成角的余弦值;
时,求异面直线BF与CD所成角的余弦值;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 为何值时,二面角A -A1D - C的平面角为600.
为何值时,二面角A -A1D - C的平面角为600.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.若
| ||||||||||||
B.向量
| ||||||||||||
| C.空间任意两个向量共面 | ||||||||||||
D.若
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com