
| 年龄段(岁) | [60,70) | [70,80) | [80,90) | [90,99) |
| 人数(人) | 125 | 75 | 25 | 5 |
分析 (1)采用分层抽样的方法抽,求出各阶段人数的比例,即可求出21人中80岁及以上老人应抽多少人.
(2)直接根据组合的性质从21人中随机抽取2人除以90岁及以上老人可得概率;
(3)根据县60岁以上、百岁以下的人口占比13.8%,计算本县户籍60岁各阶段人数.每月领取55元基本养老金,再加外享受高龄老人生活补贴计算总和政府执行此项补贴措施的年度预算.
解答 解:由题意,随机抽取230人,60-70的比例为$\frac{25}{46}$,70-80的比例为$\frac{15}{46}$,80-90的比例为$\frac{5}{46}$,90以上比例为$\frac{1}{46}$.
(1)采用分层抽样70岁及以上老人,抽21人,80岁及以上老人应抽$\frac{30}{105}×21=6$人.
(2)抽21人,80-90应抽$\frac{25}{105}×21$=5人,90以上的为1人.随机抽取2人,抽到90岁及以上老人的概率为1-$\frac{{C}_{5}^{2}}{{C}_{6}^{2}}$=$\frac{1}{3}$.
(3)在60万人,该县60岁以上、百岁以下的人口占比13.8%,
可得60岁以上百岁以下的人口为:600000×13.8%=82800人,百岁及以上的老人15人;
60岁及以上居民,每月领取55元基本养老金:82815×55=4554825元.
80岁及以上老年人额外享受高龄老人生活补贴:
①百岁及以上老年人:15×345=5175元.
②90岁及以上、百岁以下老年人,每人每月发放200元:82800×$\frac{1}{46}×200$=360000.
③80岁及以上、90岁以下老年人,每人每月发放100元:82800×$\frac{5}{46}×100$=9000000.
∴政府执行此项补贴措施的年度预算为:(4554825+5175+360000+9000000)×12个月=167040万元.
点评 本题考查了样本的数字特征及频率分布表的应用,计算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
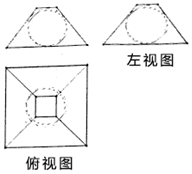 如图是某几何体挖去一部分后得到的三视图,其中主视图和左视图相同都是一个等腰梯形及它的内切圆,俯视图中有两个边长分别为2和8的正方形且图中的圆与主视图圆大小相等并且圆心为两个正方形的中心.问该几何体的体积是( )
如图是某几何体挖去一部分后得到的三视图,其中主视图和左视图相同都是一个等腰梯形及它的内切圆,俯视图中有两个边长分别为2和8的正方形且图中的圆与主视图圆大小相等并且圆心为两个正方形的中心.问该几何体的体积是( )| A. | $\frac{420-32π}{3}$ | B. | $\frac{336-32π}{3}$ | C. | $\frac{168-4π}{3}$ | D. | $\frac{168\sqrt{2}-64\sqrt{2}π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(3)>e2f(1) | B. | f(3)<ef(2) | C. | f(4)<e4f(0) | D. | f(4)<e5f(-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -16 | B. | -8 | C. | 16 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36 | B. | 16 | C. | 20 | D. | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com