
已知函数f(x)= sin
sin cos
cos +sin2
+sin2 (其中ω>0,0<φ<
(其中ω>0,0<φ< ).其图象的两个相邻对称中心的距离为
).其图象的两个相邻对称中心的距离为 ,且过点
,且过点 .
.
(1)函数f(x)的解析式;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,a= ,S△ABC=2
,S△ABC=2 ,角C为锐角.且满足f
,角C为锐角.且满足f =
= ,求c的值.
,求c的值.
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-x6练习卷(解析版) 题型:选择题
设函数f(x)=sin  ,则下列结论正确的是( ).
,则下列结论正确的是( ).
①f(x)的图象关于直线x= 对称;②f(x)的图象关于点
对称;②f(x)的图象关于点 对称;③f(x)的图象向左平移
对称;③f(x)的图象向左平移 个单位,得到一个偶函数的图象;④f(x)的最小正周期为π,且在
个单位,得到一个偶函数的图象;④f(x)的最小正周期为π,且在 上为增函数
上为增函数
A.①③ B.②④ C.①③④ D.③
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-x1练习卷(解析版) 题型:选择题
设函数f(x)的零点为x1,函数g(x)=4x+2x-2的零点为x2,若|x1-x2|> ,则f(x)可以是( ).
,则f(x)可以是( ).
A.f(x)=2x- B.f(x)=-x2+x-
B.f(x)=-x2+x-
C.f(x)=1-10x D.f(x)=ln (8x-2)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-d4练习卷(解析版) 题型:解答题
已知函数f(x)=sin  +2cos2x-1(x∈R).
+2cos2x-1(x∈R).
(1)求函数f(x)的最小正周期及单调递增区间;
(2)在△ABC中,三内角A,B,C的对边分别为a,b,c,已知函数f(x)的图象经过点 ,b,a,c成等差数列,且
,b,a,c成等差数列,且 ·
·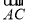 =9,求a的值.
=9,求a的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练2-2练习卷(解析版) 题型:解答题
现有甲、乙两个靶.某射手向甲靶射击两次,每次命中的概率为 ,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为
,每命中一次得1分,没有命中得0分;向乙靶射击一次,命中的概率为 ,命中得2分,没有命中得0分,该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
,命中得2分,没有命中得0分,该射手每次射击的结果相互独立.假设该射手完成以上三次射击.
(1)求该射手恰好命中两次的概率;
(2)求该射手的总得分X的分布列及数学期望E(X);
(3)求该射手向甲靶射击比向乙靶射击多击中一次的概率.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练2-1练习卷(解析版) 题型:解答题
已知函数f(x)=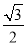 sin ωx-sin2
sin ωx-sin2 +
+ (ω>0)的最小正周期为π.
(ω>0)的最小正周期为π.
(1)求ω的值及函数f(x)的单调递增区间;
(2)当x∈ 时,求函数f(x)的取值范围.
时,求函数f(x)的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练1-9练习卷(解析版) 题型:选择题
设F1,F2分别是双曲线 =1(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P,使(
=1(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P,使( +
+ )·
)· =0,O为坐标原点,且
=0,O为坐标原点,且 =
= |
| |,则双曲线的离心率为( ).
|,则双曲线的离心率为( ).
A.  +1 B.
+1 B. 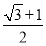 C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练1-9练习卷(解析版) 题型:选择题
已知椭圆 =1(a>b>0)的一个焦点为F,若椭圆上存在一个P点,满足以椭圆短轴为直径的圆与线段PF相切于该线段的中点,则该椭圆的离心率为( ).
=1(a>b>0)的一个焦点为F,若椭圆上存在一个P点,满足以椭圆短轴为直径的圆与线段PF相切于该线段的中点,则该椭圆的离心率为( ).
A.  B.
B.  C.
C. 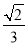 D.
D. 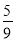
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练1-6练习卷(解析版) 题型:选择题
已知等差数列{an}满足2a2- +2a12=0,且{bn}是等比数列,若b7=a7,则b5b9=( )
+2a12=0,且{bn}是等比数列,若b7=a7,则b5b9=( )
A.2 B.4 C.8 D.16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com