
| A. | 2$\sqrt{3}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,所以球心是底面三角形的中心.然后求出三角形的边长,再求体积.
解答 解:正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,所以球心是底面三角形的中心.
设球的半径为R=1,底面三角形的边长为a,
$\frac{2}{3}×\frac{\sqrt{3}}{2}a$=1⇒a=$\sqrt{3}$
该正三棱锥的体积:$\frac{1}{3}×\frac{\sqrt{3}}{2}×(\sqrt{3})^{2}×1$=$\frac{\sqrt{3}}{4}$
故选:C
点评 本题考查了正棱锥体积公式、三角形重心定理、球大圆的定义等相关知识点,属基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是某班全体学生外出时乘车、步行、骑车的人数分布直方图和扇形分布图(两图都不完整),则下列结论中错误的是( )
如图是某班全体学生外出时乘车、步行、骑车的人数分布直方图和扇形分布图(两图都不完整),则下列结论中错误的是( )| A. | 该班总人数为50人 | B. | 步行人数为30人 | ||
| C. | 骑车人数占总人数的20% | D. | 乘车人数是骑车人数的2.5倍 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{2}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 17 | C. | 26 | D. | 2016 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
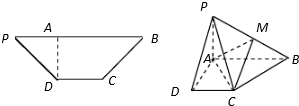 已知等腰梯形PDCB中,PB=3,DC=1,PD=BC=$\sqrt{2}$,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD.
已知等腰梯形PDCB中,PB=3,DC=1,PD=BC=$\sqrt{2}$,A为PB边上一点,且PA=1,将△PAD沿AD折起,使平面PAD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com