Question

7．已知三棱锥P-ABC中，底面△ABC是边长为3的等边三角形，侧棱长都相等，半径为$\sqrt{7}$的球O过三棱锥P-ABC的四个顶点，则点P到面ABC的距离为$\sqrt{7}±2$．

Answer 1

分析 设P在底面的射影是E，则E为底面正三角形的中心．连接AE并延长交BC于D，则三棱锥P-ABC的外接球的球心O在PE上，连接OA，在Rt△AOE中算出OE=2，由PE=PO±OE得答案．

解答 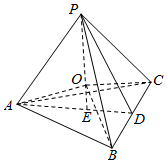解：根据题意，三棱锥P-ABC是正三棱锥，设P在底面的射影是E，则E为底面正三角形的中心．
连接AE并延长交BC于D，则三棱锥P-ABC的外接球的球心O在PE上，连接OA，
∵△ABC是边长为3的等边三角形，
∴AE=$\frac{2}{3}AD=\frac{2}{3}\sqrt{{3}^{2}-（\frac{3}{2}）^{2}}=\frac{2}{3}×\frac{3}{2}\sqrt{3}=\sqrt{3}$，
又AO=$\sqrt{7}$，
∴$OE=\sqrt{O{A}^{2}-A{E}^{2}}=\sqrt{（\sqrt{7}）^{2}-（\sqrt{3}）^{2}}=2$，
∴PE=PO±OE=$\sqrt{7}±2$．
故答案为：$\sqrt{7}±2$．

点评 本题考查空间中点线面位置关系的应用，考查空间想象能力和思维能力，着重考查了正棱锥的性质和球内接多面体的计算等知识，属于中档题．