
分析 (I)利用导数的几何意义可得切线的斜率,进而得出k.
(Ⅱ)解法一:即证:lnx-ax3-x>lnx-x ex,即证:ax3+x<x ex,因为x>0,即证:ax2+1<ex,设h(x)=ex-ax2-1,h'(x)=ex-2ax,令h''(x)=ex-2a.对a分类讨论:( i)当$a≤\frac{1}{2}$时,( ii)当$a>\frac{1}{2}$时,利用导数研究h′(x)及其h(x)的单调性即可证明.
解法二:即证:lnx-ax3-x>lnx-x ex,即证:x ex>ax3+x,因为x>0,即证:ex-ax2-1>0,因为$a≤\frac{e}{2}$,即证${e^x}-\frac{e}{2}{x^2}-1>0$,令$k(x)={e^x}-\frac{e}{2}{x^2}-1$,k'(x)=ex-ex,k''(x)=ex-e>0,利用导数研究其单调性即可证明.
解答 (Ⅰ)解:由已知得f(1)=0,所以切点坐标(1,0)(1分)
又f(1)=0-a-1=0,得a=-1,(2分)
$f'(x)=\frac{1}{x}+3{x^2}-1$,所以k=f'(1)=1+3-1=3.(4分)
(Ⅱ)解法一:即证:lnx-ax3-x>lnx-x ex,即证:ax3+x<x ex,
因为x>0,即证:ax2+1<ex,(5分)
设h(x)=ex-ax2-1,h'(x)=ex-2ax,令h''(x)=ex-2a
( i)当$a≤\frac{1}{2}$时,h''(x)>0,h'(x)单调递增,h'(x)>h'(0)=1,
h(x)单调递增,h(x)>h(0)=0,满足题意;(7分)
( ii)当$a>\frac{1}{2}$时,h''(x)=ex-2a=0,解得x=ln2a,
当x∈(0,ln2a),h''(x)<0,h'(x)单调递减,
当x∈(ln2a,+∞),h''(x)<0,h'(x)单调递增,(9分)
此时$h'{(x)_{min}}=h'(ln2a)={{e}^{ln2a}}-2aln2a=2a(1-ln2a)$,(10分)
因为$a≤\frac{e}{2}$,1-ln2a≥0,即h'(x)min>0,h(x)单调递增,h(x)>h(0)=0,满足题意;(11分)
综上可得,当$a≤\frac{e}{2}$时,f(x)>lnx-xex.(12分)
解法二:即证:lnx-ax3-x>lnx-x ex,即证:x ex>ax3+x,
因为x>0,即证:ex-ax2-1>0,(5分)
因为$a≤\frac{e}{2}$,即证${e^x}-\frac{e}{2}{x^2}-1>0$,(8分)
令$k(x)={e^x}-\frac{e}{2}{x^2}-1$,k'(x)=ex-ex,k''(x)=ex-e>0,k'(x)单调递增,k'(x)>1,k(x)单调递增,k(x)>k(0)=0.
所以${{e}^x}>\frac{e}{2}{x^2}+1≥a{x^2}+1$,故原不等式得证.(12分)
点评 本题考查了利用导数研究函数的单调性极值与最值、方程与不等式的解法、分类讨论方法、等价转化方法、分析法,考查了推理能力与计算能力,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{72.8}{81}$ | B. | $\frac{182}{81}$ | C. | $\frac{364}{81}$ | D. | $\frac{91}{81}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
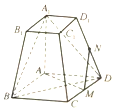 如图,在四棱台ABCD-A1B1C1D1中,底面ABCD为平行四边形,∠BAD=120°,M为CD上的点.且∠A1AB=∠A1AD=90°,AD=A1A=2,A1B1=DM=1.
如图,在四棱台ABCD-A1B1C1D1中,底面ABCD为平行四边形,∠BAD=120°,M为CD上的点.且∠A1AB=∠A1AD=90°,AD=A1A=2,A1B1=DM=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2$\overrightarrow{AD}$ | B. | 2$\overrightarrow{AD}$ | C. | -3$\overrightarrow{AD}$ | D. | 3$\overrightarrow{AD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)是偶函数 | |
| B. | f(x)的递减区间是(-1,1) | |
| C. | 若方程f(x)+k=0有三个不同的实数根,则-2≤k≤0 | |
| D. | 任意的a>0,$f(lga)+f(lg\frac{1}{a})=0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$-1 | B. | 2-$\sqrt{2}$ | C. | $\sqrt{2}$+1 | D. | 2+$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com