
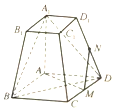
 如图,在四棱台ABCD-A1B1C1D1中,底面ABCD为平行四边形,∠BAD=120°,M为CD上的点.且∠A1AB=∠A1AD=90°,AD=A1A=2,A1B1=DM=1.
如图,在四棱台ABCD-A1B1C1D1中,底面ABCD为平行四边形,∠BAD=120°,M为CD上的点.且∠A1AB=∠A1AD=90°,AD=A1A=2,A1B1=DM=1.分析 (1)利用勾股定理逆定理得出AM⊥CD,即AM⊥AB,结合AM⊥AA1得出AM⊥平面AA1B1B,于是AM⊥A1B;
(2)建立空间坐标系,根据MN与平面A1BD所成角的大小确定N点位置,从而得出DN的长.
解答  证明:(1)在平行四边形ABCD中,∠BAD=120°,∴∠ADM=60°,
证明:(1)在平行四边形ABCD中,∠BAD=120°,∴∠ADM=60°,
在△ADM中,AD=2,DM=1,∴$AM=\sqrt{A{D^2}+D{M^2}-2•AD•DM•cos∠ADM}$=$\sqrt{3}$,
可得AD2=AM2+DM2,∴AM⊥CD.
又CD∥AB,∴AM⊥AB,
∵∠A1AB=∠A1AD=90°,∴A1A⊥AB,A1A⊥AD.
又∵AB∩AD=A,AB,AD?平面ABCD,
∴AA1⊥ABCD,又AM?平面ABCD,
∴AM⊥AA1.又∵AB∩AA1=A,AB,AA1?平面AA1B1B,
∴AM⊥平面AA1B1B.又∵A1B?平面AA1B1B,
∴AM⊥A1B.
解:(2)∵M为CD的中点,DM=1,∴CD=2,
所以四边形ABCD为菱形.
分别以AB,AM,AA1为x轴,y轴,z轴,建立如图所示的空间直角坐标系A-xyz,
则点${A_1}({0,0,2}),B({2,0,0}),D({-1,\sqrt{3},0}),{D_1}({-\frac{1}{2},\frac{{\sqrt{3}}}{2},2})$.
∴$\overrightarrow{D{D_1}}=({\frac{1}{2},-\frac{{\sqrt{3}}}{2},2}),\overrightarrow{BD}=({-3,\sqrt{3},0}),\overrightarrow{{A_1}B}=({2,0,-2})$.
设平面A1BD的一个法向量为$\overrightarrow n=({x,y,z})$,则有$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{BD}=0\\ \overrightarrow n•\overrightarrow{{A_1}B}=0\end{array}\right.$,
∴$\left\{\begin{array}{l}-3x+\sqrt{3}y=0\\ 2x-2z=0\end{array}\right.$,令x=1,则$\overrightarrow n=({1,\sqrt{3},1})$,
设$\overrightarrow{DN}=λ\overrightarrow{D{D_1}}=({\frac{λ}{2},-\frac{{\sqrt{3}}}{2}λ,2λ})({λ∈[{0,1}]})$,∴$\overrightarrow{MN}=\overrightarrow{MD}+\overrightarrow{DN}=({\frac{λ}{2}-1,-\frac{{\sqrt{3}}}{2}λ,2λ})$,
∴$\frac{1}{{\sqrt{35}}}=|{cos\left?{\overrightarrow n,\overrightarrow{MN}}\right>}|=|{\frac{{\frac{λ}{2}-1-\frac{3}{2}λ+2λ}}{{\sqrt{5}•\sqrt{{{({\frac{λ}{2}-1})}^2}+{{({\frac{{\sqrt{3}}}{2}λ})}^2}+{{({2λ})}^2}}}}}|$,
∴$\frac{1}{{\sqrt{7}}}=\frac{{|{λ-1}|}}{{\sqrt{5{λ^2}-λ+1}}}$,∴2λ2-13λ+6=0,
∴$λ=\frac{1}{2}$或λ=6(舍去).
∴$DN=\frac{1}{2}D{D_1}=\frac{{\sqrt{5}}}{2}$.
点评 本题考查了线面垂直的判定,空间向量与空间角的计算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | 3 | C. | 8 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,0<φ<π)的图象如图所示,
函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,0<φ<π)的图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{8}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
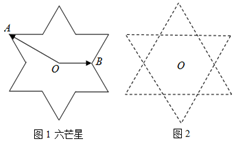 如图2,“六芒星”是由两个全等正三角形组成,中心重合于点O且三组对边分别平行.点A,B是“六芒星”(如图1)的两个顶点,动点P在“六芒星”上(内部以及边界),若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,则x+y的取值范围是( )
如图2,“六芒星”是由两个全等正三角形组成,中心重合于点O且三组对边分别平行.点A,B是“六芒星”(如图1)的两个顶点,动点P在“六芒星”上(内部以及边界),若$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,则x+y的取值范围是( )| A. | [-4,4] | B. | $[{-\sqrt{21},\sqrt{21}}]$ | C. | [-5,5] | D. | [-6,6] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $0<m≤3-2\sqrt{2}$或$m≥3+2\sqrt{2}$ | B. | $m<3-2\sqrt{2}$或$m>3+2\sqrt{2}$ | ||
| C. | $0<m<3-2\sqrt{2}$或$m>3+2\sqrt{2}$ | D. | $m≤3-2\sqrt{2}$或$m≥3+2\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com