
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
分析 设双曲线的另一焦点为F′,根据双曲线的定义得MF′=3a+c,在△MFF′中,由余弦定理得MF′2=MF2+FF′2-2MF•FF′cos60°,即4a2+3ac-c2=0,解得4a=c,即$\frac{c}{a}=4$即可
解答 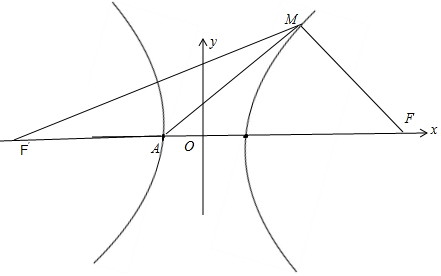 解:如图所示,∵MF=FA,∠MFA=60°,
解:如图所示,∵MF=FA,∠MFA=60°,
∴△MFA是等边三角形.
则有AF=a+c,MF=a+c,
设双曲线的另一焦点为F′,根据双曲线的定义得MF′=3a+c,
在△MFF′中,由余弦定理得MF′2=MF2+FF′2-2MF•FF′cos60°,
即4a2+3ac-c2=0,解得4a=c,即$\frac{c}{a}=4$,
∴双曲线C的离心率为4.
故选:C.
点评 本题考查了双曲线的方程、定义、离心率,考查了转化思想、数形结合思想,属于中档题.


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
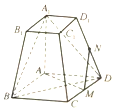 如图,在四棱台ABCD-A1B1C1D1中,底面ABCD为平行四边形,∠BAD=120°,M为CD上的点.且∠A1AB=∠A1AD=90°,AD=A1A=2,A1B1=DM=1.
如图,在四棱台ABCD-A1B1C1D1中,底面ABCD为平行四边形,∠BAD=120°,M为CD上的点.且∠A1AB=∠A1AD=90°,AD=A1A=2,A1B1=DM=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)是偶函数 | |
| B. | f(x)的递减区间是(-1,1) | |
| C. | 若方程f(x)+k=0有三个不同的实数根,则-2≤k≤0 | |
| D. | 任意的a>0,$f(lga)+f(lg\frac{1}{a})=0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com