
【题目】经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出15条作样本,经检测得各条鱼的汞含量的茎叶图(以小数点前的数字为茎,小数点后一位数字为叶)如图.《中华人民共和国环境保护法》规定食品的汞含量不得超过1.0ppm.
(Ⅰ)检查人员从这15条鱼中,随机抽出3条,求3条中恰有1条汞含量超标的概率;
(Ⅱ)若从这批数量很大的鱼中任选3条鱼,记ξ表示抽到的汞含量超标的鱼的条数.以此15条鱼的样本数据来估计这批数量很大的鱼的总体数据,求ξ的分布列及数学期望Eξ.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|.
(1)若不等式f(x+ ![]() )≥2m+1(m>0)的解集为(﹣∞,﹣2]∪[2,+∞),求实数m的值;
)≥2m+1(m>0)的解集为(﹣∞,﹣2]∪[2,+∞),求实数m的值;
(2)若不等式f(x)≤2y+ ![]() +|2x+3|,对任意的实数x,y∈R恒成立,求实数a的最小值.
+|2x+3|,对任意的实数x,y∈R恒成立,求实数a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
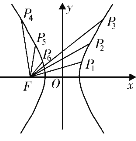
【题目】如图所示,F为双曲线C:![]() ﹣
﹣![]() =1的左焦点,双曲线C上的点Pi与P7﹣i(i=1,2,3)关于y轴对称,则|P1F|+|P2F|+|P3F|﹣|P4F|﹣|P5F|﹣|P6F|的值是( )
=1的左焦点,双曲线C上的点Pi与P7﹣i(i=1,2,3)关于y轴对称,则|P1F|+|P2F|+|P3F|﹣|P4F|﹣|P5F|﹣|P6F|的值是( )
A. 9 B. 16 C. 18 D. 27
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=![]() .
.
(Ⅰ)求证:AC⊥平面BEH;
(Ⅱ)求直线PA与平面ABC所成角的正弦值.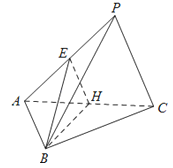
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“嫦娥奔月,举国欢庆”,据科学计算,运载“神六”的“长征二号”系列火箭,在点火第一秒钟通过的路程为2 km,以后每秒钟通过的路程都增加2 km,在达到离地面210 km的高度时,火箭与飞船分离,则这一过程大约需要的时间是______秒.
【答案】14
【解析】
设出每一秒钟的路程为一数列,由题意可知此数列为等差数列,然后根据等差数列的前n项和的公式表示出离地面的高度,让高度等于210列出关于n的方程,求出方程的解即可得到n的值.
设每一秒钟通过的路程依次为a1,a2,a3,…,an,
则数列{an}是首项a1=2,公差d=2的等差数列,
由求和公式有na1+![]() =210,即2n+n(n﹣1)=210,
=210,即2n+n(n﹣1)=210,
解得n=14,
故答案为:14
【点睛】
在解决等差、等比数列的运算问题时,有两个处理思路,一是利用基本量,将多元问题简化为一元问题,虽有一定量的运算,但思路简洁,目标明确;二是利用等差、等比数列的性质是两种数列基本规律的深刻体现,应有意识地去应用.但在应用性质时要注意性质的前提条件,有时需要进行适当变形. 在解决等差、等比数列的运算问题时,经常采用“巧用性质、整体考虑、减少运算量”的方法.
【题型】填空题
【结束】
16
【题目】已知直线l:![]() +
+![]() =1,M是直线l上的一个动点,过点M作x轴和y轴的垂线,垂足分别为A,B,点P是线段AB的靠近点A的一个三等分点,点P的轨迹方程为______.
=1,M是直线l上的一个动点,过点M作x轴和y轴的垂线,垂足分别为A,B,点P是线段AB的靠近点A的一个三等分点,点P的轨迹方程为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}、等差数列{bn},满足a1>0,b1=a1﹣1,b2=a2 , b3=a3且数列{an}唯一.
(1)求数列{an},{bn}的通项公式;
(2)求数列{anbn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A、B为抛物线C:![]() 上两点,A与B的中点的横坐标为2,直线AB的斜率为1.
上两点,A与B的中点的横坐标为2,直线AB的斜率为1.
(Ⅰ)求抛物线C的方程;
(Ⅱ)直线![]() 交x轴于点M,交抛物线C:
交x轴于点M,交抛物线C:![]() 于点P,M关于点P的对称点为N,连结ON并延长交C于点H.除H以外,直线MH与C是否有其他公共点?请说明理由.
于点P,M关于点P的对称点为N,连结ON并延长交C于点H.除H以外,直线MH与C是否有其他公共点?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱柱ABCD-A1B1C1D1中,底面边长为2![]() ,侧棱长为4,E,F分别是棱AB,BC的中点,EF∩BD=G.求证:平面B1EF⊥平面BDD1B1.
,侧棱长为4,E,F分别是棱AB,BC的中点,EF∩BD=G.求证:平面B1EF⊥平面BDD1B1.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA=PB=AB=BC=2,∠CBA=∠PBC=60°,Q为线段BC的中点.
(1)求证:PA⊥BC;
(2)求点Q到平面PAC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com