
分析 利用三角函数的图象变换可求得g(x)=sin(2x+θ-2φ),依题意可得(2x+θ)-(2x+θ-2φ)=kπ(k∈Z),对k赋值,观察选项即可.
解答 解:∵g(x)=f(x-φ)=sin[2(x-φ)+θ]=sin(2x+θ-2φ),
又f(x)=sin(2x+θ)与g(x)=sin(2x+θ-2φ)的图象的对称轴重合,
∴(2x+θ)-(2x+θ-2φ)=kπ(k∈Z),
∴φ=$\frac{kπ}{2}$(k∈Z),
故答案为:$\frac{kπ}{2}$(k∈Z)
点评 本题考查函数y=Asin(ωx+φ)的图象变换,考查正弦函数的图象的对称性,分析得到(2x+θ)-(2x+θ-2φ)=kπ(k∈Z)是关键,考查转化思想,属于基本知识的考查.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.
在如图所示的多面体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
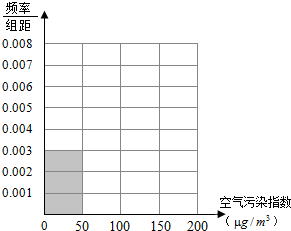 空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2015年1月某日某省x个监测点数据统计如下:
空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染;当空气污染指数为200~300时,空气质量级别为五级,空气质量状况属于重度污染;当空气污染指数为300以上时,空气质量级别为六级,空气质量状况属于严重污染.2015年1月某日某省x个监测点数据统计如下:| 空气污染指数 (单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | k<32? | B. | k<63? | C. | k<64? | D. | k<70? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | arcsin-$\frac{2}{5}$ | B. | arcsin$\frac{2}{5}$或(arcsin$\frac{2}{5}$)+π | ||
| C. | arcsin$\frac{2}{5}$ | D. | arcsin(-$\frac{2}{5}$)或arcsin$\frac{2}{5}$-π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com