
| A. | $\sqrt{2013}$-1 | B. | $\sqrt{2014}$-1 | C. | $\sqrt{2015}$-1 | D. | $\sqrt{2015}$+1 |
分析 函数f(x)=xa的图象过点(4,2),代入解出a,可得f(x)=$\sqrt{x}$.an=$\sqrt{n+1}-\sqrt{n}$,再利用“裂项求和”即可得出.
解答 解:函数f(x)=xa的图象过点(4,2),
∴2=4a,解得a=$\frac{1}{2}$.
∴f(x)=$\sqrt{x}$.
令an=$\frac{1}{f(n+1)+f(n)}$=$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}-\sqrt{n}$,
∴数列{an}的前n项和为Sn=$(\sqrt{2}-1)$+$(\sqrt{3}-\sqrt{2})$+…+($\sqrt{n+1}-\sqrt{n}$)=$\sqrt{n+1}$-1,
则S2014=$\sqrt{2015}$-1.
故选:C.
点评 本题考查了函数的性质、数列的“裂项求和”,考查了推理能力与计算能力,属于中档题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
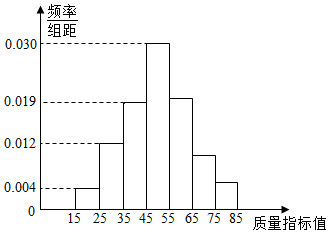 从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.
从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 过点(-1,0)的一切直线 | B. | 过点(1,0)的一切直线 | ||
| C. | 过点(1,0)且不垂直于x轴的一切直线 | D. | 过点(1,0)且除x轴外的一切直线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com