
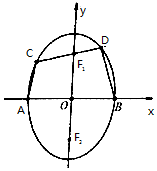
 ��֪F1��F2�ֱ�����Բ$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1��a��b��0�����ϣ��½��㣬A��B�ֱ�Ϊ��Բ�����Ҷ��㣬����Բ���Ͻ���F1��ֱ����x���Ϸ����ֽ���Բ��C��D���㣬��F2CD���ܳ�Ϊ8������Բ��������Ϊ$\frac{\sqrt{3}}{2}$��
��֪F1��F2�ֱ�����Բ$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1��a��b��0�����ϣ��½��㣬A��B�ֱ�Ϊ��Բ�����Ҷ��㣬����Բ���Ͻ���F1��ֱ����x���Ϸ����ֽ���Բ��C��D���㣬��F2CD���ܳ�Ϊ8������Բ��������Ϊ$\frac{\sqrt{3}}{2}$������ ��1��������Բ�Ķ��壬��4a=8��a=2�����������ʹ�ʽ���������c����b2=a2-c2=1�����������Բ���̣�
��2����ֱ��CD�ķ��̣�������Բ���̣�����Τ�ﶨ�����������ĵ����Լ������S�����ֵ��
��� �⣺��1������Բ�Ķ���حCF1ح+حCF2ح=2a��حDF1ح+حDF2ح=2a����F2CD���ܳ�ΪΪ4a��
��4a=8����a=2��
����Բ��������e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$��c=$\sqrt{3}$��b2=a2-c2=1��
����Բ�ı����̣�$\frac{{y}^{2}}{4}+{x}^{2}=1$��
��2���ɣ�1��֪��F1��0��$\sqrt{3}$��������ֱ��y=kx+$\sqrt{3}$��C��x1��y1����D��x2��y2����
$\left\{\begin{array}{l}{y=kx+\sqrt{3}}\\{\frac{{y}^{2}}{4}+{x}^{2}=1}\end{array}\right.$���������k2+4��x2+2$\sqrt{3}$kx-1=0��
��x1+x2=-$\frac{2\sqrt{3}k}{{k}^{2}+4}$��x1x2=-$\frac{1}{{k}^{2}+4}$��
حx1-x1ح=$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$\frac{4\sqrt{{k}^{2}+1}}{{k}^{2}+4}$����y1��0��y2��0����0��k2��3��
��y1+y2=k��x1+x2��+2$\sqrt{3}$=$\frac{8\sqrt{3}}{{k}^{2}+4}$��
���ı���ABCD�����S��S=SAOC+SBOD+SOCD=$\frac{1}{2}$��$\frac{8\sqrt{3}}{{k}^{2}+4}$+$\frac{1}{2}$��$\sqrt{3}$��$\frac{4\sqrt{{k}^{2}+1}}{{k}^{2}+4}$=$\frac{2\sqrt{3}��\sqrt{{k}^{2}+1}+2��}{{k}^{2}+4}$��
��t=$\sqrt{{k}^{2}+1}$+2��t��[3��4����
��S=$\frac{2\sqrt{3}t}{��t-2��^{2}+3}$=$\frac{2\sqrt{3}}{t+\frac{7}{t}-4}$��t��[3��4���ϵ����ݼ���
��S�ʣ�$\frac{8\sqrt{3}}{7}$��$\frac{3\sqrt{3}}{2}$]��
��S�����ֵ$\frac{3\sqrt{3}}{2}$��
���� ���⿼����Բ�ı����̣�ֱ������Բ��λ�ù�ϵ������Τ�ﶨ�����ҳ���ʽ����������������Բ��Ӧ�ã�������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��=$\frac{2}{3}$����=$\frac{��}{12}$ | B�� | ��=$\frac{2}{3}$����=-$\frac{11��}{12}$ | C�� | ��=$\frac{1}{3}$����=-$\frac{11��}{24}$ | D�� | ��=$\frac{1}{3}$����=$\frac{7��}{24}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
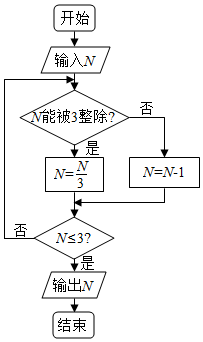
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
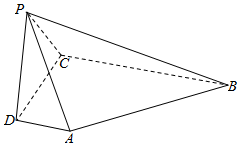 ��ͼ��������P-ABCD�У�AD��ƽ��PDC��AD��BC��PD��PB��AD=1��BC=3��CD=4��PD=2��
��ͼ��������P-ABCD�У�AD��ƽ��PDC��AD��BC��PD��PB��AD=1��BC=3��CD=4��PD=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 0 | C�� | 2 | D�� | 8 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com