
分析 (Ⅰ)用数学归纳法即可证明,
(Ⅱ)构造函数,利用导数判断函数的单调性,把数列问题转化为函数问题,即可证明,
(Ⅲ)由$\frac{{x}_{n}{x}_{n+1}}{2}$≥2xn+1-xn得$\frac{1}{{x}_{n+1}}$-$\frac{1}{2}$≥2($\frac{1}{{x}_{n}}$-$\frac{1}{2}$)>0,继续放缩即可证明
解答 解:(Ⅰ)用数学归纳法证明:xn>0,
当n=1时,x1=1>0,成立,
假设当n=k时成立,则xk>0,
那么n=k+1时,若xk+1<0,则0<xk=xk+1+ln(1+xk+1)<0,矛盾,
故xn+1>0,
因此xn>0,(n∈N*)
∴xn=xn+1+ln(1+xn+1)>xn+1,
因此0<xn+1<xn(n∈N*),
(Ⅱ)由xn=xn+1+ln(1+xn+1)得xnxn+1-4xn+1+2xn=xn+12-2xn+1+(xn+1+2)ln(1+xn+1),
记函数f(x)=x2-2x+(x+2)ln(1+x),x≥0
∴f′(x)=$\frac{2{x}^{2}+x}{x+1}$+ln(1+x)>0,
∴f(x)在(0,+∞)上单调递增,
∴f(x)≥f(0)=0,
因此xn+12-2xn+1+(xn+1+2)ln(1+xn+1)≥0,
故2xn+1-xn≤$\frac{{x}_{n}{x}_{n+1}}{2}$;
(Ⅲ)∵xn=xn+1+ln(1+xn+1)≤xn+1+xn+1=2xn+1,
∴xn≥$\frac{1}{{2}^{n-1}}$,
由$\frac{{x}_{n}{x}_{n+1}}{2}$≥2xn+1-xn得$\frac{1}{{x}_{n+1}}$-$\frac{1}{2}$≥2($\frac{1}{{x}_{n}}$-$\frac{1}{2}$)>0,
∴$\frac{1}{{x}_{n}}$-$\frac{1}{2}$≥2($\frac{1}{{x}_{n-1}}$-$\frac{1}{2}$)≥…≥2n-1($\frac{1}{{x}_{1}}$-$\frac{1}{2}$)=2n-2,
∴xn≤$\frac{1}{{2}^{n-2}}$,
综上所述$\frac{1}{{2}^{n-1}}$≤xn≤$\frac{1}{{2}^{n-2}}$.
点评 本题考查了数列的概念,递推关系,数列的函数的特征,导数和函数的单调性的关系,不等式的证明,考查了推理论证能力,分析解决问题的能力,运算能力,放缩能力,运算能力,属于难题


科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.
如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
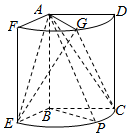 如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点.
如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是$\widehat{DF}$的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
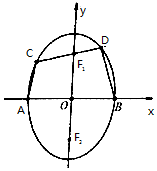 已知F1、F2分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上,下焦点,A,B分别为椭圆的左、右顶点,过椭圆的上焦点F1的直线在x轴上方部分交椭圆于C、D两点,△F2CD的周长为8,若椭圆的离心率为$\frac{\sqrt{3}}{2}$.
已知F1、F2分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的上,下焦点,A,B分别为椭圆的左、右顶点,过椭圆的上焦点F1的直线在x轴上方部分交椭圆于C、D两点,△F2CD的周长为8,若椭圆的离心率为$\frac{\sqrt{3}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com