
分析 (1)由已知可得$f(x)=\sqrt{2}sin({x-\frac{π}{4}})$,由函数y=Asin(ωx+φ)的图象变换规律即可得解.
(2)令sinx-cosx=t,则可求sin2x=1-t2,可得h(x)=f(x)+g(x)=φ(t)=-t2+t+1,由t的范围,结合二次函数的性质可求值域.
解答 (本题满分为12分)
解:(1)$f(x)=\sqrt{2}sin({x-\frac{π}{4}})$…(2分)
故先将y=sin2x的图象上所有点纵坐标不变,横坐标伸长到原来的两倍得到y=sinx的图象,
再将y=sinx的图象上所有点横坐标不变,纵坐标伸长到原来的$\sqrt{2}$倍得到$y=\sqrt{2}sinx$的图象,
再把所得图象向左平移$\frac{π}{4}$个单位,即得到$y=\sqrt{2}sin({x-\frac{π}{4}})$的图象.…(5分)
(2)令sinx-cosx=t,则1-2sinxcosx=t2
故sin2x=1-t2
故h(x)=f(x)+g(x)=φ(t)=-t2+t+1…(7分)
由(1)知,$t∈[{-\sqrt{2},\sqrt{2}}],所以φ(t)在[{-\sqrt{2},\frac{1}{2}}]递增,[{\frac{1}{2},\sqrt{2}}]递减$,
所以$φ(t)∈[{-\sqrt{2}-1,\frac{5}{4}}]$,故h(x)的值域为$[{-\sqrt{2}-1,\frac{5}{4}}]$….(12分)
点评 本题值域考查了函数y=Asin(ωx+φ)的图象变换,二次函数的图象和性质的综合应用,考查了转化思想和数形结合思想,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
 如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.
如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
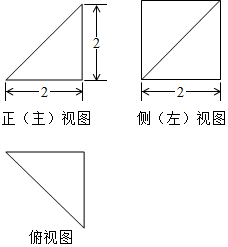
| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 乙可以知道四人的成绩 | B. | 丁可以知道四人的成绩 | ||
| C. | 乙、丁可以知道对方的成绩 | D. | 乙、丁可以知道自己的成绩 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ω=$\frac{2}{3}$,φ=$\frac{π}{12}$ | B. | ω=$\frac{2}{3}$,φ=-$\frac{11π}{12}$ | C. | ω=$\frac{1}{3}$,φ=-$\frac{11π}{24}$ | D. | ω=$\frac{1}{3}$,φ=$\frac{7π}{24}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com