
分析 逐项判断.①利用正弦定理易得;②先平方在利用基本不等式即可;③由等差数列的函数特征易得;④易知当q=1时,结论不正确.
解答 解:
①由正弦定理,当sinA>sinB时,由 a>b,故有A>B,所以①为真;
②$(\sqrt{a+3}+\sqrt{b+2})^{2}=9+2\sqrt{(a+3)(b+2)}$≤9+(a+3)+(b+2)=18,所以$\sqrt{a+3}+\sqrt{b+2}≤3\sqrt{2}$“=”当且仅当“$a=\frac{3}{2},b=\frac{5}{2}$”成立,故②为真;
③由等差数列的通项公式的函数特征知③正确;
④易知,当q=1时结论不正确.
总上可得①②③正确.
故答案为:①②③.
点评 本题考查了正弦定理,基本不等式,等差数列的通项以及等比数列的前n项和问题.其中第2个命题的判断是本题难点.属于中档题.


科目:高中数学 来源: 题型:解答题
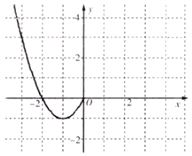 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示,根据图象:
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示,根据图象:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 连江一中第49届田径运动会提出了“我运动、我阳光、我健康、我快乐”的口号,某同学要设计一张如图所示的竖向张贴的长方形海报进行宣传,要求版心面积为162dm2(版心是指图中的长方形阴影部分,dm为长度单位分米),上、下两边各空2dm,左、右两边各空1dm.
连江一中第49届田径运动会提出了“我运动、我阳光、我健康、我快乐”的口号,某同学要设计一张如图所示的竖向张贴的长方形海报进行宣传,要求版心面积为162dm2(版心是指图中的长方形阴影部分,dm为长度单位分米),上、下两边各空2dm,左、右两边各空1dm.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com