
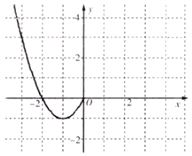
 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示,根据图象:
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.现已画出函数f(x)在y轴左侧的图象,如图所示,根据图象:分析 (1)根据偶函数的图象关于y轴对称,可作出f(x)的图象,由图象可得f(x)的单调递增区间;
(2)令x>0,则-x<0,根据条件可得f(-x)=x2-2x,利用函数f(x)是定义在R上的偶函数,可得f(x)=f(-x)=x2-2x,从而可得函数f(x)的解析式;
(3)先求出抛物线对称轴x=2a--1,然后分当2a+1≤1时,当1<2a+1≤2时,当2a+1>2时三种情况,根据二次函数的增减性解答.
解答 解:(1)如图,根据偶函数的图象关于y轴对称,可作出f(x)的图象,(2分),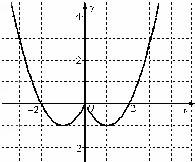
则f(x)的单调递增区间为(-1,0),(1,+∞);(5分)
(2)令x>0,则-x<0,∴f(-x)=x2-2x
∵函数f(x)是定义在R上的偶函数,
∴f(x)=f(-x)=x2-2x
∴解析式为f(x)=$\left\{\begin{array}{l}{{x}^{2}+2x,x≤0}\\{{x}^{2}-2x,x>0}\end{array}\right.$(10分)
(3)g(x)=x2-2x-4ax+2,对称轴为x=2a+1,
当2a+1≤1时,g(1)=1-4a为最小;
当1<2a+1≤3时,g(2a+1)=-4a2-4a+1为最小;
当2a+1>3时,g(3)=5-12a为最小;
∴g(x)min=$\left\{\begin{array}{l}{1-4a,a≤0}\\{-4{a}^{2}-4a+1,0<a<1}\\{5-12a,a≥1}\end{array}\right.$.(16分)
点评 本题考查函数图象的作法,考查函数解析式的确定与函数的单调性,考查学生分析解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 12 | C. | 13 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p:?α∈R,使幂函数y=xα图象经过第四象限;命题q:在锐角△ABC中,sinA>cosB,则p∧q为真 | |
| B. | 命题:“正切函数y=tan x在定义域内为增函数”的逆否命题为真 | |
| C. | 在区间(a,b)连续的函数f(x),f(a)•f(b)<0是f(x)在区间(a,b)内有零点的充要条件 | |
| D. | 命题p:函数f(x)=x2-2x仅有两个零点,则?p是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com