
【题目】2018年3月3日至20日中华人民共和国第十三届全国人民代表大会第一次会议和中国人民政治协商会议第十三届全国委员会第一次会议在北京胜利召开,两会是年度中国政治生活中的一件大事,受到了举国上下和全世界的广泛关注.为及时宣传国家政策,贯彻两会精神,某校举行了全国两会知识竞赛,为了解本次竞赛成绩情况,随机抽取了部分学生的成绩(得分均为整数,满分![]() 分,最低分不低于
分,最低分不低于![]() 分)进行统计,得出频率分布表如下:
分)进行统计,得出频率分布表如下:
组号 | 分组 | 频数 | 频率 |
第1组 |
|
|
|
第2组 |
|
|
|
第3组 |
|
|
|
第4组 |
|
|
|
第5组 |
|
|
|
合计 |
|
| |
(1)求表中![]() 、
、![]() 、
、![]() 、
、![]() 的值;
的值;
(2)若从成绩较好的第![]() 、
、![]() 、
、![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人担任两会知识宣传员,再从这
人担任两会知识宣传员,再从这![]() 人中随机选出
人中随机选出![]() 人负责整理两会相关材料,求这
人负责整理两会相关材料,求这![]() 人中至少有
人中至少有![]() 人来自第
人来自第![]() 组的概率.
组的概率.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)由频率分布表得:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)由题意可得第![]() 、
、![]() 、
、![]() 组应分别抽取
组应分别抽取![]() 人、
人、![]() 人、
人、![]() 人.则从
人.则从![]() 为同学中抽
为同学中抽![]() 为同学有
为同学有![]() 种可能,其中第
种可能,其中第![]() 组至少有
组至少有![]() 人入选有
人入选有![]() 种,则这
种,则这![]() 人中至少有
人中至少有![]() 人来自第
人来自第![]() 组的概率为
组的概率为![]() .
.
详解:(1)由频率分布表得:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(2)∵第![]() 、
、![]() 、
、![]() 组共有
组共有![]() 名学生,
名学生,
∴利用分层抽样在![]() 名学生中抽取
名学生中抽取![]() 名学生,每组分别为:
名学生,每组分别为:
第![]() 组:
组:![]() 人,第4组:
人,第4组:![]() 人,第5组:
人,第5组:![]() 人,
人,
∴第![]() 、
、![]() 、
、![]() 组应分别抽取
组应分别抽取![]() 人、
人、![]() 人、
人、![]() 人.
人.
记第![]() 组的
组的![]() 位同学为
位同学为![]() ,第
,第![]() 组的
组的![]() 位同学为
位同学为![]() 、
、![]() ,第
,第![]() 组的
组的![]() 位同学为
位同学为![]() 、
、![]() 、
、![]() ,则从
,则从![]() 为同学中抽
为同学中抽![]() 为同学有
为同学有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 种可能,
种可能,
其中第![]() 组至少有
组至少有![]() 人入选的有
人入选的有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共
,共![]() 种,
种,
∴这![]() 人中至少有
人中至少有![]() 人来自第
人来自第![]() 组的概率为
组的概率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,![]() 平面
平面![]() .
.
(1)证明:![]() 平面
平面![]() ;
;
(2)过点![]() 作一平行于平面
作一平行于平面![]() 的截面,画出该截面,说明理由,并求夹在该截面与平面
的截面,画出该截面,说明理由,并求夹在该截面与平面![]() 之间的几何体的体积.
之间的几何体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 为钝角三角形且垂直于底面
为钝角三角形且垂直于底面![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若直线![]() 与底面
与底面![]() 所成的角为60°,求二面角
所成的角为60°,求二面角![]() 余弦值.
余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 及函数
及函数![]() (a,b,c∈R),若a>b>c且a+b+c=0.
(a,b,c∈R),若a>b>c且a+b+c=0.
(1)证明:f(x)的图像与g(x)的图像一定有两个交点;
(2)请用反证法证明:![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市疾控中心流感监测结果显示,自![]() 年
年![]() 月起,该市流感活动一度出现上升趋势,尤其是
月起,该市流感活动一度出现上升趋势,尤其是![]() 月以来,呈现快速增长态势,截止目前流感病毒活动度仍处于较高水平,为了预防感冒快速扩散,某校医务室采取积极方式,对感染者进行短暂隔离直到康复.假设某班级已知
月以来,呈现快速增长态势,截止目前流感病毒活动度仍处于较高水平,为了预防感冒快速扩散,某校医务室采取积极方式,对感染者进行短暂隔离直到康复.假设某班级已知![]() 位同学中有
位同学中有![]() 位同学被感染,需要通过化验血液来确定感染的同学,血液化验结果呈阳性即为感染,呈阴性即未被感染.下面是两种化验方法: 方案甲:逐个化验,直到能确定感染同学为止;
位同学被感染,需要通过化验血液来确定感染的同学,血液化验结果呈阳性即为感染,呈阴性即未被感染.下面是两种化验方法: 方案甲:逐个化验,直到能确定感染同学为止;
方案乙:先任取![]() 个同学,将它们的血液混在一起化验,若结果呈阳性则表明感染同学为这
个同学,将它们的血液混在一起化验,若结果呈阳性则表明感染同学为这![]() 位中的
位中的![]() 位,后再逐个化验,直到能确定感染同学为止;若结果呈阴性则在另外
位,后再逐个化验,直到能确定感染同学为止;若结果呈阴性则在另外![]() 位同学中逐个检测;
位同学中逐个检测;
(1)求依方案甲所需化验次数等于方案乙所需化验次数的概率;
(2)![]() 表示依方案甲所需化验次数,
表示依方案甲所需化验次数,![]() 表示依方案乙所需化验次数,假设每次化验的费用都相同,请从经济角度考虑那种化验方案最佳.
表示依方案乙所需化验次数,假设每次化验的费用都相同,请从经济角度考虑那种化验方案最佳.
查看答案和解析>>
科目:高中数学 来源: 题型:
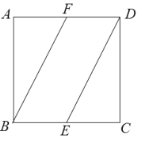
【题目】如图所示,在正方形![]() 中,点
中,点![]() ,
,![]() 分别为边
分别为边![]() ,
,![]() 的中点,将
的中点,将![]() 沿
沿![]() 所在直线进行翻折,将
所在直线进行翻折,将![]() 沿
沿![]() 所在直线进行翻折,在翻折的过程中,
所在直线进行翻折,在翻折的过程中,
①点![]() 与点
与点![]() 在某一位置可能重合;②点
在某一位置可能重合;②点![]() 与点
与点![]() 的最大距离为
的最大距离为![]() ;
;
③直线![]() 与直线
与直线![]() 可能垂直; ④直线
可能垂直; ④直线![]() 与直线
与直线![]() 可能垂直.
可能垂直.
以上说法正确的个数为( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水,任意转动这个正方体,则水面在容器中的形状可以是:(1)三角形;(2)长方形;(3)正方形;(4)正六边形.其中正确的结论是____________.(把你认为正确的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com