
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
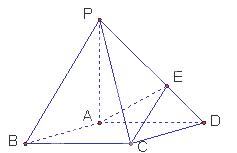
如图,在底面是菱形的四棱锥P—ABCD中,∠ABC=600,PA=AC=a,PB=PD=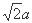 ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.
(I)证明PA⊥平面ABCD;
(II)求以AC为棱,EAC与DAC为面的二面角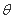 的大小;
的大小;
(Ⅲ)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
若椭圆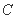 的方程为
的方程为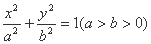 ,
,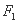 、
、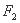 是它的左、右焦点,椭圆
是它的左、右焦点,椭圆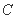 过点
过点 ,且离心率为
,且离心率为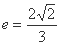 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆的左右顶点为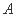 、
、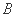 ,直线
,直线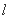 的方程为
的方程为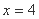 ,
,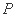 是椭圆上任一点,直线
是椭圆上任一点,直线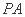 、
、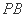 分别交直线
分别交直线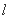 于
于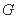 、
、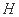 两点,求
两点,求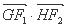 的值;
的值;
(Ⅲ)过点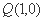 任意作直线
任意作直线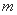 (与
(与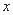 轴不垂直)与椭圆
轴不垂直)与椭圆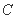 交于
交于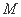 、
、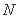 两点,与
两点,与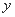 轴交于
轴交于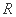 点
点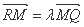 ,
,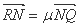 .证明:
.证明: 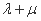 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
某校高二年级的一次数学考试中,为了分析学生的得分情况,随机抽取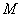 名同学的成绩,数据的分组统计表如下:
名同学的成绩,数据的分组统计表如下:
| 分组 | 频数 | 频率 | 频率/组距 |
| (40,50] | 2 | 0.02 | 0.002 |
| (50,60] | 4 | 0.04 | 0.004[来源:学科网] |
| (60,70] | 11 | 0.11 | 0.011 |
| (70,80] | 38 | 0.3 | 0.038 |
| (80,90] |
|
|
|
| (90,100] | 11 | 0.11 | 0.011 |
| 合计 |
|
|
|
(1)求出 表中
表中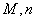 的值;
的值;
(2)根据上表,请在画出频率分布直方图;
(3)为了了解某些同学在数学学习中存在的问题,现从样本中分数在 中的6位同学中任意抽取2人进行调查,求分数在
中的6位同学中任意抽取2人进行调查,求分数在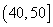 和
和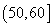 中各有一人的概率.
中各有一人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
数列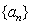 的前
的前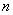 项和为
项和为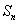 ,且满足
,且满足 ,
,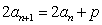 (
( 为常数,
为常数, ).
).
(Ⅰ)若 ,求
,求 ;
;
(Ⅱ)若数列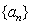 是等比数列,求实数
是等比数列,求实数 的值.
的值.
(Ⅲ)是否存在实数 ,使得数列
,使得数列 满足:可以从中取出无限多项并按原来的先后次序排成一个等差数列?若存在,求出所有满足条件的
满足:可以从中取出无限多项并按原来的先后次序排成一个等差数列?若存在,求出所有满足条件的 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com