
数列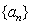 的前
的前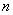 项和为
项和为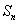 ,且满足
,且满足 ,
,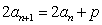 (
( 为常数,
为常数, ).
).
(Ⅰ)若 ,求
,求 ;
;
(Ⅱ)若数列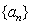 是等比数列,求实数
是等比数列,求实数 的值.
的值.
(Ⅲ)是否存在实数 ,使得数列
,使得数列 满足:可以从中取出无限多项并按原来的先后次序排成一个等差数列?若存在,求出所有满足条件的
满足:可以从中取出无限多项并按原来的先后次序排成一个等差数列?若存在,求出所有满足条件的 的值;若不存在,说明理由.
的值;若不存在,说明理由.
解:(Ⅰ)因为  ,
,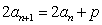 ,
,
所以 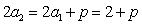 ,
,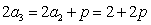 .
.
因为  ,
,
所以 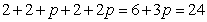 ,即
,即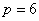 .
.
所以 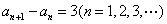 .
.
所以 数列 是以1为首项,3为公差的等差数列.
是以1为首项,3为公差的等差数列.
所以 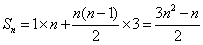 .
.
(Ⅱ)若数列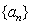 是等比数列,则
是等比数列,则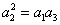 .
.
由(Ⅰ)可得: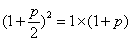 .
.
解得: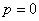 .
.
当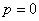 时,由
时,由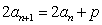 得:
得: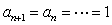 .
.
显然,数列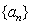 是以1为首项,1为公比的等比数列.
是以1为首项,1为公比的等比数列.
所以 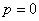 .
.
(Ⅲ)当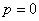 时,由(Ⅱ)知:
时,由(Ⅱ)知: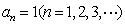 .
.
所以  ,即数列
,即数列 就是一个无穷等差数列.
就是一个无穷等差数列.
所以 当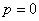 时,可以得到满足题意的等差数列.
时,可以得到满足题意的等差数列.
当 时,因为
时,因为  ,
,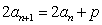 ,即
,即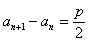 ,
,
所以 数列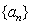 是以1为首项,
是以1为首项,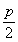 为公差的等差数列.
为公差的等差数列.
所以 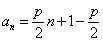 .
.
下面用反证法证明:当 时,数列
时,数列 中不能取出无限多项并按原来次序排列而成等差数列.
中不能取出无限多项并按原来次序排列而成等差数列.
假设存在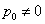 ,从数列
,从数列 中可以取得满足题意的无穷等差数列,不妨记为
中可以取得满足题意的无穷等差数列,不妨记为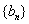 . 设数列
. 设数列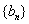 的公差为
的公差为 .
.
①当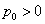 时,
时,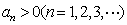 .
.
所以 数列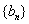 是各项均为正数的递减数列.
是各项均为正数的递减数列.
所以 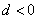 .
.
因为 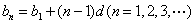 ,
,
所以 当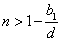 时,
时,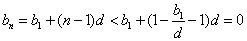 ,这与
,这与 矛盾.
矛盾.
②当 时,令
时,令 ,解得:
,解得: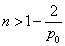 .
.
所以 当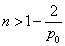 时,
时,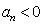 恒成立.
恒成立.
所以 数列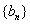 必然是各项均为负数的递增数列.
必然是各项均为负数的递增数列.
所以 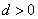 .
.
因为 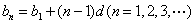 ,
,
所以 当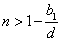 时,
时, ,这与
,这与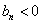 矛盾.
矛盾.
综上所述,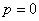 是唯一满足条件的
是唯一满足条件的 的值.
的值.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
用反证法证明命题:“三角形的内角至多有一个钝角”时,假设正确的是 ( )
 假设至少有一个钝角
假设至少有一个钝角  假设至少有两个钝角
假设至少有两个钝角
 假设没有一个钝角
假设没有一个钝角  假设没有一个钝角或假设至少有两个钝角
假设没有一个钝角或假设至少有两个钝角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com