
分析 (1)由f(x)=(x-k)ex,求导f′(x)=(x-k+1)ex,令f′(x)=0,求得x=k-1,令f′(x)<0,解得函数的单调递减区间,f′(x)>0,解得函数的单调递增区间,根据函数的单调性即可求得f(x)的极值;
(2)当k-1≤1时,f(x)在[1,2]单调递增,f(x)的最小值为f(1),当k-1≥2时,f(x)在[1,2]单调递减,f(x)的最小值为f(2),当1<k-1<2时,则x=k-1时,f(x)取最小值,最小值为:-ek-1;
(3)由g(x)=(2x-2k+1)ex,求导g′(x)=(2x-2k+3)ex,当g′(x)<0,解得:x<k-$\frac{3}{2}$,求得函数的单调递减区间,当g′(x)>0,解得:x>k-$\frac{3}{2}$,求得函数的单调递增区间,由题意可知g(x)≥λ,?x∈[0,1]恒成立,等价于g(k-$\frac{3}{2}$)=-2e${\;}^{k-\frac{3}{2}}$≥λ,由-2e${\;}^{k-\frac{3}{2}}$≥λ,对?k∈[$\frac{3}{2}$,$\frac{5}{2}$]恒成立,根据函数的单调性,即可求得实数λ的取值范围.
解答 解:(1)f(x)=(x-k)ex(k∈R),求导f′(x)=(x-k)ex+ex=(x-k+1)ex,
令f′(x)=0,解得:x=k-1,
当x<k-1时,f′(x)<0,
当x>k-1时,f′(x)>0,
| x | (-∞,k-1) | k-1 | (k-1,+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↓ | -e-k-1 | ↑ |
点评 本题考查利用到时研究函数的单调性和在闭区间上的最值,考查函数导数的运算,考查转化思想,考查计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
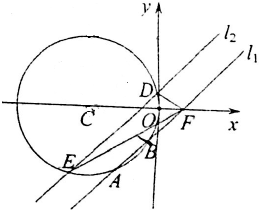 已知直线l1:y=x-1与圆C:(x+a)2+y2=a2(a>0)相交于A、B两点,|AB|=2,直线l2∥l1,直线l2与圆C相交于D、E两点.
已知直线l1:y=x-1与圆C:(x+a)2+y2=a2(a>0)相交于A、B两点,|AB|=2,直线l2∥l1,直线l2与圆C相交于D、E两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com