
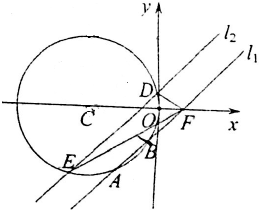
 已知直线l1:y=x-1与圆C:(x+a)2+y2=a2(a>0)相交于A、B两点,|AB|=2,直线l2∥l1,直线l2与圆C相交于D、E两点.
已知直线l1:y=x-1与圆C:(x+a)2+y2=a2(a>0)相交于A、B两点,|AB|=2,直线l2∥l1,直线l2与圆C相交于D、E两点.分析 (I)求出圆心C到直线l1的距离,利用勾股定理建立方程,求出圆心坐标,即可求圆C的标准方程;
(Ⅱ)依题意可设直线l2的方程为x-y+m=0(m≠-1),而由点到直线的距离公式得:${d_2}=\frac{{|{-3+m}|}}{{\sqrt{{1^2}+{{({-1})}^2}}}}=\frac{{|{m-3}|}}{{\sqrt{2}}}=\frac{3}{2}\sqrt{2}$,即可求直线l2的方程;
(Ⅲ)由∠CFD=∠CFE知:kFD+kFE=0即有$\frac{y_1}{{{x_2}-1}}+\frac{y_2}{{{x_2}-1}}=0$,利用韦达定理,即可求直线l2的方程.
解答 解:(I)可知圆C的圆心坐标为(-a,0),半径为r=a
圆心C到直线l1的距离为${d_1}=\frac{{|{-a-1}|}}{{\sqrt{{1^2}+{{({-1})}^2}}}}=\frac{{|{a+1}|}}{{\sqrt{2}}}$
由垂径定理知:${r^2}-{d_1}^2={({\frac{1}{2}|{AB}|})^2}$
即有:${a^2}-\frac{{{{({a+1})}^2}}}{2}=1$(a>0)解得:a=3
故所求圆C的标准方程为(x+3)2+y2=9
(II)易知:若△CDE为直角三角形,则∠DCE=90°
又CD=CE=r=3可知△CDE为等腰直角三角形
由垂径定理:圆心C到直线l2的距离${d_2}=\frac{{\sqrt{2}}}{2}r=\frac{3}{2}\sqrt{2}$
依题意可设直线l2的方程为x-y+m=0(m≠-1)
而由点到直线的距离公式得:${d_2}=\frac{{|{-3+m}|}}{{\sqrt{{1^2}+{{({-1})}^2}}}}=\frac{{|{m-3}|}}{{\sqrt{2}}}=\frac{3}{2}\sqrt{2}$
解得:m=0或m=6故所求直线l2的方程为x-y=0或x-y+6=0
(III)可知直线l1与x轴交点F的坐标为(1,0),依题意可设直线l2的方程为y=x+t
将其与圆的标准方程(x+3)2+y2=9联立整理可得:2x2+(2t+6)x+t2=0
设D、E两点坐标分别为(x1,y1),(x2,y2)由韦达定理可得:${x_1}+{x_2}=-\frac{2t+6}{2}=-t-3$,${x_1}•{x_2}=\frac{t^2}{2}$
由∠CFD=∠CFE知:kFD+kFE=0即有$\frac{y_1}{{{x_2}-1}}+\frac{y_2}{{{x_2}-1}}=0$,
得(x2-1)y1+(x1-1)y2=(x2-1)(x1+t)+(x1-1)(x2+t)=2x1x2+(t-1)(x1+x2)-2t
于是有$2•\frac{t^2}{2}+({t-1})({-t-3})-2t=0$得$t=\frac{3}{4}$
故所求直线l2的方程为$y=x+\frac{3}{4}$,即4x-4y+3=0.
点评 本题考查圆的方程,考查直线与圆的位置关系,考查韦达定理的运用,难度大.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | b<c<a | C. | a<c<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | $4\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com