
分析 (1)函数y=f(x)-c的零点可转化为函数f(x)=|a2x2-1|+ax的图象与直线y=c的交点问题,运用绝对值意义和二次函数图象及二次方程韦达定理,即可得到所求值;
(2)运用分段函数表示f(x),结合图象分析函数的单调性,即可得到f(x)在[-1,1]的最大值.
解答 解:(1)函数y=f(x)-c的零点可转化为
函数f(x)=|a2x2-1|+ax的图象与直线y=c的交点问题.
当a2x2≥1即|x|≥-$\frac{1}{a}$时,f(x)=a2x2+ax-1=(ax+$\frac{1}{2}$)2-$\frac{5}{4}$;
当a2x2<1即|x|<-$\frac{1}{a}$时,f(x)=-a2x2+ax+1=-(ax-$\frac{1}{2}$)2+$\frac{5}{4}$.
显然当1<c<$\frac{5}{4}$时,y=f(x)-c有4个零点,
依次设为x1,x2,x3,x4,
则x1,x4是方程a2x2+ax-1=c的2个根,从而${x_1}+{x_4}=-\frac{1}{a}$,
由x2,x3是方程-a2x2+ax+1=c的2个根,知x2+x3=$\frac{1}{a}$,
从而x1+x2+x3+x4=0.
(2)f(x)=$\left\{\begin{array}{l}{{a}^{2}{x}^{2}+ax-1,|x|≥-\frac{1}{a}}\\{-{a}^{2}{x}^{2}+ax+1,|x|<-\frac{1}{a}}\end{array}\right.$,
结合图形分析可得f(x)在$({-∞,\frac{1}{a}}]$,$[{\frac{1}{2a},-\frac{1}{a}}]$上单调递减,
在$[{\frac{1}{a},\frac{1}{2a}}],[{-\frac{1}{a},+∞})$上单调递减,此时M(a)=f($\frac{1}{2a}$)=$\frac{5}{4}$.
当$-1<\frac{1}{a}$,即a<-1时,f(x)在[-1,$\frac{1}{a}$],[$\frac{1}{2a}$,-$\frac{1}{a}$]上单调递减,
f(x)在$[{\frac{1}{a},\frac{1}{2a}}],[{-\frac{1}{a},1}]$上单调递增,此时
M(a)=max{f(-1),f($\frac{1}{2a}$),f(1)}
=max{a2-a-1,$\frac{5}{4}$,a2+a-1}
=max{a2-a-1,$\frac{5}{4}$}=$\left\{\begin{array}{l}{{a}^{2}-a-1,a≤\frac{1-\sqrt{10}}{2}}\\{\frac{5}{4},\frac{1-\sqrt{10}}{2}<a<-1}\end{array}\right.$,
综上述,
M(a)=$\left\{\begin{array}{l}{-{a}^{2}-a+1,-\frac{1}{2}≤a<0}\\{\frac{5}{4},a<-\frac{1}{2}}\\{{a}^{2}-a-1,a≤\frac{1-\sqrt{10}}{2}}\end{array}\right.$.
点评 本题考查函数零点问题的解法,注意运用数形结合方法,考查化简运算能力,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
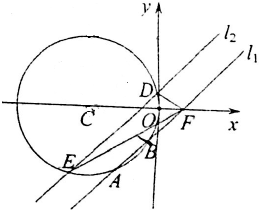 已知直线l1:y=x-1与圆C:(x+a)2+y2=a2(a>0)相交于A、B两点,|AB|=2,直线l2∥l1,直线l2与圆C相交于D、E两点.
已知直线l1:y=x-1与圆C:(x+a)2+y2=a2(a>0)相交于A、B两点,|AB|=2,直线l2∥l1,直线l2与圆C相交于D、E两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com