
分析 (Ⅰ)求出函数f(x)的导数,解关于x的不等式,求出函数的单调区间即可;
(Ⅱ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(Ⅲ)根据函数的单调性得到$|{f({x_1})-f({x_2})}|≤f(4)-f(1)=\frac{27}{4}-6ln2$,从而求出m的范围即可.
解答 解:函数f(x)的定义域为(0,+∞),
(Ⅰ)当a=0时,$f(x)=-\frac{1}{x}-2lnx$,$f'(x)=\frac{1}{x^2}-\frac{2}{x}=\frac{1-2x}{x^2}$. …(1分)
当$0<x<\frac{1}{2}$时,f'(x)>0,函数f(x)在区间$({0\;\;,\;\;\frac{1}{2}})$上单调递增;…(2分)
当$x>\frac{1}{2}$时,f'(x)<0,函数f(x)在区间$({\frac{1}{2}\;\;,\;\;+∞})$上单调递减;…(3分)
所以,当$x=\frac{1}{2}$时,函数f(x)取得极大值为$f({\frac{1}{2}})=2ln2-2$;不存在极小值. …(4分)
(Ⅱ)当a>0时,$f'(x)=2a+\frac{1}{x^2}-\frac{2+a}{x}=\frac{{2a{x^2}-({2+a})x+1}}{x^2}$=$\frac{{({2x-1})({ax-1})}}{x^2}$. …(5分)
由f'(x)=0,得$x=\frac{1}{2}$或$x=\frac{1}{a}$. …(6分)
①当$\frac{1}{a}<\frac{1}{2}$,即a>2时,由f'(x)>0,得$0<x<\frac{1}{a}$或$x>\frac{1}{2}$;
由f'(x)<0,得$\frac{1}{a}<x<\frac{1}{2}$,
所以函数f(x)在区间$({0\;\;,\;\;\frac{1}{a}})$,$({\frac{1}{2}\;\;,\;\;+∞})$上单调递增,在区间$({\frac{1}{a}\;\;,\;\;\frac{1}{2}})$上单调递减;…(7分)
②当$\frac{1}{a}=\frac{1}{2}$,即a=2时,f'(x)≥0在(0,+∞)恒成立,
所以函数f(x)在区间(0,+∞)上单调递增;…(8分)
③当$\frac{1}{a}>\frac{1}{2}$,即0<a<2时,由f'(x)>0,得$0<x<\frac{1}{2}$或$x>\frac{1}{a}$;由f'(x)<0,得$\frac{1}{2}<x<\frac{1}{a}$,
所以函数f(x)在区间$({0\;\;,\;\;\frac{1}{2}})$,$({\frac{1}{a}\;\;,\;\;+∞})$上单调递增,在区间$({\frac{1}{2}\;\;,\;\;\frac{1}{a}})$上单调递减. …(9分)
综上所述,当a>2时,函数f(x)在区间$({0\;\;,\;\;\frac{1}{a}})$,$({\frac{1}{2}\;\;,\;\;+∞})$上单调递增,
在区间$({\frac{1}{a}\;\;,\;\;\frac{1}{2}})$上单调递减;
当a=2时,函数函数f(x)在区间(0,+∞)上单调递增;
当0<a<2时,函数f(x)在区间$({0\;\;,\;\;\frac{1}{2}})$,$({\frac{1}{a}\;\;,\;\;+∞})$上单调递增,
在区间$({\frac{1}{2}\;\;,\;\;\frac{1}{a}})$上单调递减.…(10分)
(Ⅲ)当a=1时,由(Ⅱ)知,函数f(x)在区间[1,4]上是增函数,
所以$|{f({x_1})-f({x_2})}|≤f(4)-f(1)=\frac{27}{4}-6ln2$,…(11分)
因为对于任意的x1,x2∈[1,4],都有$|{f({x_1})-f({x_2})}|<\frac{27}{4}-2mln2$成立,
所以$\frac{27}{4}-6ln2<\frac{27}{4}-2mln2$恒成立,…(12分)
解得m<3,…(13分)
故m的取值范围为(-∞,3). …(14分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,是一道综合题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | $(1,\frac{3}{2}]$ | C. | $[\frac{3}{2},2)$ | D. | (0,1)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 34 | C. | 42 | D. | 55 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{20}$ | B. | $\frac{1}{15}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20.09万元 | B. | 20.50万元 | C. | 20.91万元 | D. | 21.33万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
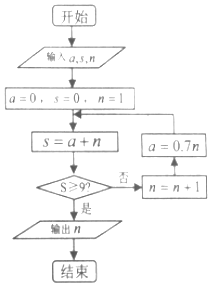 我国古代数学典籍《九章算术》“盈不足”中有一道问题:“今有垣高九尺,瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺,问几何日相逢?”现用程序框图描述,如图所示,则输出的结果n=( )
我国古代数学典籍《九章算术》“盈不足”中有一道问题:“今有垣高九尺,瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺,问几何日相逢?”现用程序框图描述,如图所示,则输出的结果n=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com