
分析 (1)根据tanθ=$\frac{y}{x}$可得直线l1极坐标.利用x=ρcosθ,y=ρsinθ带入可得曲线C的极坐标方程.
(2)由题意,设A(ρ1,θ1),联立方程组求解,同理,设利用直线的极坐标的几何意义求解即可.
解答 解:(1)直线l1的方程为y=$\sqrt{3}$x,
可得:tanθ=$\frac{y}{x}$=$\sqrt{3}$,
∴直线l1的极坐标方程为$θ=\frac{π}{3}$.
曲线C的普通方程为(x-1)2+y2=3,
又∵x=ρcosθ,y=ρsinθ,
所以曲线C的极坐标方程为ρ2-2ρcosθ-2=0(0≤θ≤π)
(2)由题意,设A(ρ1,θ1),则有$\left\{\begin{array}{l}{ρ-2ρcosθ-2=0}\\{θ=\frac{π}{3}}\end{array}\right.$,解得:${ρ}_{1}=2,{θ}_{1}=\frac{π}{3}$
设B(ρ2,θ2),则有$\left\{\begin{array}{l}{2ρsin(θ+\frac{π}{3})+3\sqrt{3}=0}\\{θ=\frac{π}{3}}\end{array}\right.$,解得:${ρ}_{2}=-3,{θ}_{2}=\frac{π}{3}$
故得|AB|=|ρ1-ρ2|=5.
点评 本题主要考查了参数方程,极坐标方程的转换,以及利用极坐标的几何意义求解长度问题.属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
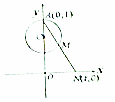 把周长为1的圆的圆心C放在y轴,顶点A(0,1),一动点M从A开始顺时针绕圆运动一周,记走过的弧长$\widehat{AM}$=x,直线AM与x轴交于点N(t,0),则函数t=f(x)的大致图象( )
把周长为1的圆的圆心C放在y轴,顶点A(0,1),一动点M从A开始顺时针绕圆运动一周,记走过的弧长$\widehat{AM}$=x,直线AM与x轴交于点N(t,0),则函数t=f(x)的大致图象( )| A. | 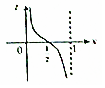 | B. | 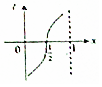 | C. |  | D. | 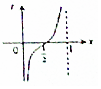 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com