
分析 如图所示,过C作CE⊥AB,垂足为E.在Rt△CED中,可得CE=$\sqrt{3}$,∠ECD=30°.在Rt△CEB中,由CB$≥\sqrt{6}$,可得cos∠BCE=$\frac{CE}{CB}$≤$\frac{\sqrt{2}}{2}$,即可得出.
解答 解:如图所示,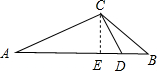 过C作CE⊥AB,垂足为E.
过C作CE⊥AB,垂足为E.
在Rt△CED中,∠ADC=60°,CD=2,
∴CE=2sin60°=$\sqrt{3}$,∠ECD=30°.
在Rt△CEB中,∵CB$≥\sqrt{6}$,
则cos∠BCE=$\frac{CE}{CB}$≤$\frac{\sqrt{3}}{\sqrt{6}}$=$\frac{\sqrt{2}}{2}$,
∴90°>∠BCE≥45°.
∴∠BCD≥15°,
∴∠ACD≤120°-15°=105°.
故答案为:105°.
点评 本题考查了直角三角形的边角关系、三角函数的单调性,考查了推理能力与计算能力,属于中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | -12 | B. | -1 | C. | 0 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $?x∈({-∞,\frac{π}{4}}),tanx≤1$ | |
| B. | 设l,m表示不同的直线,α表示平面,若m∥l且m⊥α,则l∥α | |
| C. | 利用计算机产生0和l之间的均匀随机数m,则事件“3m-1≥0”发生的概率为$\frac{1}{3}$ | |
| D. | “a>0,b>0”是“$\frac{b}{a}+\frac{a}{b}$≥2”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 34 | C. | 42 | D. | 55 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$钱 | B. | $\frac{5}{4}$钱 | C. | $\frac{6}{5}$钱 | D. | $\frac{7}{6}$钱 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{20}$ | B. | $\frac{1}{15}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
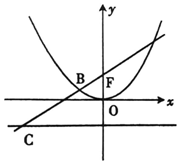 如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于AB,交其准线于点C,若|BC|=2|BF|,且|AF|=2,则p=( )
如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于AB,交其准线于点C,若|BC|=2|BF|,且|AF|=2,则p=( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2-$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com