
【题目】2019年泉州市农村电商发展迅猛,成为创新农产品交易方式、增加农民收入、引导农业供给侧结构性改革、促进乡村振兴的重要力量,成为乡村振兴的新引擎.2019年大学毕业的李想,选择回到家乡泉州自主创业,他在网上开了一家水果网店.2019年双十一期间,为了增加水果销量,李想设计了下面两种促销方案:方案一:购买金额每满120元,即可抽奖一次,中奖可获得20元,每次中奖的概率为![]() (
(![]() ),假设每次抽奖相互独立.方案二:购买金额不低于180元时,即可优惠
),假设每次抽奖相互独立.方案二:购买金额不低于180元时,即可优惠![]() 元,并在优惠后的基础上打九折.
元,并在优惠后的基础上打九折.
(1)在促销方案一中,设每10个抽奖人次中恰有6人次中奖的概率为![]() ,求
,求![]() 的最大值点
的最大值点![]() ;
;
(2)若促销方案二中,李想每笔订单得到的金额均不低于促销前总价的八折,求![]() 的最大值;
的最大值;
(3)以(1)中确定的![]() 作为
作为![]() 的值,且当
的值,且当![]() 取最大值时,若某位顾客一次性购买了360元,则该顾客应选择哪种促销方案?请说明理由.
取最大值时,若某位顾客一次性购买了360元,则该顾客应选择哪种促销方案?请说明理由.
【答案】(1)![]() ;(2)20元;(3)选择方案一,理由见解析
;(2)20元;(3)选择方案一,理由见解析
【解析】
(1) 依题意得:![]() ,利用求导,即可求出最值
,利用求导,即可求出最值
(2) 设顾客一次购买水果的促销前总价为![]() ,当
,当![]() 元时,有
元时,有![]() 恒成立,利用参变分离法,把
恒成立,利用参变分离法,把![]() 和
和![]() 分别放在不等式两边即可求解.
分别放在不等式两边即可求解.
(3)分别列出参加两种活动的方案,然后分别计算出减负金额即可判断应选择哪种促销方案
解:(1)依题意得:![]() ,
,
则![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 时取得最大值,所以
时取得最大值,所以![]() .
.
(2)设顾客一次购买水果的促销前总价为![]() ,
,
当![]() 元时,有
元时,有![]() 恒成立,
恒成立,
即![]() 恒成立,所以
恒成立,所以![]() ,故
,故![]() 的最大值为20元.
的最大值为20元.
(3)若参加活动一,顾客可抽奖三次.设X表示顾客在三次抽奖中中奖的次数,
由于顾客每次抽奖的结果相互独立,则![]() ,
,
所以![]() .
.
由于顾客每中一次可获得20元现金奖励,
因此该顾客在三次抽奖中可获得的奖励金额的均值为![]() 元,
元,
若参加活动二,顾客可得减负金额为![]() 元.
元.
又因为![]() ,所以顾客应该选择活动二.
,所以顾客应该选择活动二.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下表是我国大陆地区从2013年至2019年国内生产总值(GDP)近似值(单位:万亿元人民币)的数据表格:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
中国大陆地区GDP: (单位:万亿元人民币) |
|
|
|
|
|
|
|
![]() 为解释变量,
为解释变量,![]() 为预报变量,若以
为预报变量,若以![]() 为回归方程,则相关指数
为回归方程,则相关指数![]() ;若以
;若以![]() 为回归方程,则相关指数
为回归方程,则相关指数![]() .
.
(1)判断![]() 与
与![]() 哪一个更适宜作为国内生产总值(GDP)近似值
哪一个更适宜作为国内生产总值(GDP)近似值![]() 关于年份代号
关于年份代号![]() 的回归方程,并说明理由;
的回归方程,并说明理由;
(2)根据(1)的判断结果及表中数据,求出![]() 关于年份代号
关于年份代号![]() 的回归方程(系数精确到
的回归方程(系数精确到![]() );
);
(3)党的十九大报告中指出:从2020年到2035年,在全面建成小康社会的基础上,再奋斗15年,基本实视社会主义现代化.若到2035年底我国人口增长为![]() 亿人,假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示.
亿人,假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示.
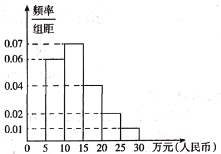
以(2)的结论为依据,预测我国在2035年底人均国民生产总值是否可以超过假设的2035年世界主要中等发达国家的人均国民生产总值平均数的估计值.
参考数据:![]() ,
,![]() .
.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: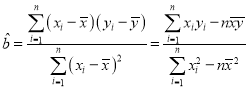 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图统计了截止到2019年年底中国电动汽车充电桩细分产品占比及保有量情况,关于这5次统计,下列说法正确的是( )
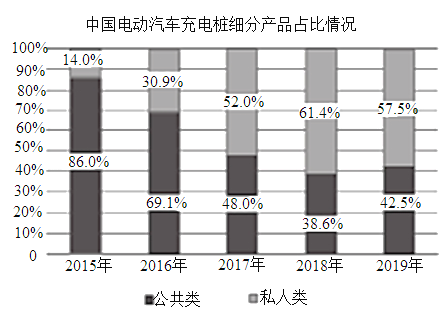
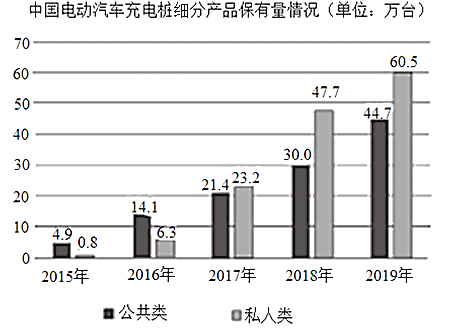
A.私人类电动汽车充电桩保有量增长率最高的年份是2018年
B.公共类电动汽车充电桩保有量的中位数是25.7万台
C.公共类电动汽车充电桩保有量的平均数为23.12万台
D.从2017年开始,我国私人类电动汽车充电桩占比均超过50%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,泉州市区的房价依旧是市民关心的话题.总体来说,二手房房价有所下降;相比二手房而言,新房市场依然强劲,价格持续升高.已知销售人员主要靠售房提成领取工资.现统计泉州市某新房销售人员2019年一年的工资情况的结果如图所示,则下列说法正确的是( )
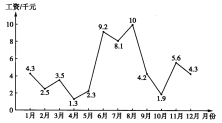
A.2019年该销售人员月工资的中位数为![]()
B.2019年该销售人员8月份的工资增长率最高
C.2019年该销售人员第一季度月工资的方差小于第二季度月工资的方差
D.2019年该销售人员第一季度月工资的平均数大于第四季度月工资的平均数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
:![]() (
(![]() )的离心率
)的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,过
,过![]() ,
,![]() 分别作两条相互垂直的直线
分别作两条相互垂直的直线![]() ,
,![]() ,分别交椭圆
,分别交椭圆![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() 四点,
四点,![]() ,
,![]() 的交点为
的交点为![]() ,三角形
,三角形![]() 面积的最大值为1.
面积的最大值为1.
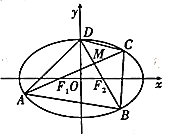
(1)求椭圆![]() 的方程;
的方程;
(2)当四边形![]() 的面积
的面积![]() 最小时,求点
最小时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为原点,抛物线![]() 的准线与y轴的交点为H,P为抛物线C上横坐标为4的点,已知点P到准线的距离为5.
的准线与y轴的交点为H,P为抛物线C上横坐标为4的点,已知点P到准线的距离为5.
(1)求C的方程;
(2)过C的焦点F作直线l与抛物线C交于A,B两点,若以AH为直径的圆过B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,且经过点
的长轴长为4,且经过点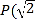 .
.
(1)求椭圆的方程;
(2)直线![]() 的斜率为
的斜率为![]() ,且与椭圆相交于
,且与椭圆相交于![]() ,
,![]() 两点(异于点
两点(异于点![]() ),过
),过![]() 作
作![]() 的角平分线交椭圆于另一点
的角平分线交椭圆于另一点![]() .证明:直线
.证明:直线![]() 与坐标轴平行.
与坐标轴平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,过点F,斜率为1的直线与抛物线C交于点A,B,且
的焦点为F,过点F,斜率为1的直线与抛物线C交于点A,B,且![]() .
.
(1)求抛物线C的方程;
(2)过点Q(1,1)作直线交抛物线C于不同于R(1,2)的两点D、E,若直线DR,ER分别交直线![]() 于M,N两点,求|MN|取最小值时直线DE的方程.
于M,N两点,求|MN|取最小值时直线DE的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com