
【题目】金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生.新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了160名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
(1)根据上表说明,能否有99%把握认为愿意参加新生接待工作与性别有关;
(2)现从参与问卷调查且愿意参加新生接待工作的学生中,采用按性别分层抽样的方法,选取10人.若从这10人中随机选取3人到火车站迎接新生,设选取的3人中女生人数为![]() ,写出
,写出![]() 的分布列,并求
的分布列,并求![]() .
.
附: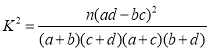 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
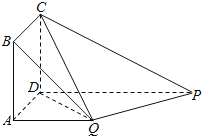
【题目】如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=![]() PD.
PD.
(1)证明:平面PQC⊥平面DCQ;
(2)求直线DQ与面PQC成角的正弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图,则下列结论中不一定正确的是( ).
注:90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生.

A. 互联网行业从业人员中90后占一半以上
B. 互联网行业中从事技术岗位的人数超过总人数的20%
C. 互联网行业中从事运营岗位的人数90后比80前多
D. 互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 为平面上
为平面上![]() 个点的集合,其中任三点不共线,任四点不共圆.一个圆被称为“好圆”是指
个点的集合,其中任三点不共线,任四点不共圆.一个圆被称为“好圆”是指![]() 中有三个点在圆上,
中有三个点在圆上,![]() 个点在圆内,
个点在圆内,![]() 个点在圆外.求证:好圆的个数与
个点在圆外.求证:好圆的个数与![]() 有相同的奇偶性.
有相同的奇偶性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com