
【题目】设![]() 为平面上
为平面上![]() 个点的集合,其中任三点不共线,任四点不共圆.一个圆被称为“好圆”是指
个点的集合,其中任三点不共线,任四点不共圆.一个圆被称为“好圆”是指![]() 中有三个点在圆上,
中有三个点在圆上,![]() 个点在圆内,
个点在圆内,![]() 个点在圆外.求证:好圆的个数与
个点在圆外.求证:好圆的个数与![]() 有相同的奇偶性.
有相同的奇偶性.
【答案】见解析
【解析】
考虑![]() 个点对
个点对![]() ,设包含点对
,设包含点对![]() 的好圆个数为
的好圆个数为![]() ,则好圆总个数应为
,则好圆总个数应为![]() (因为每个圆包含三个点对).由于
(因为每个圆包含三个点对).由于![]() 与
与![]() 同奇偶,故只须证明所有
同奇偶,故只须证明所有![]() 均为奇数即可.
均为奇数即可.
对任一点对![]() ,把在
,把在![]() 下方的任一点,比如说
下方的任一点,比如说![]() ,在上方作一点
,在上方作一点![]() ,使
,使![]() ,把
,把![]() 下方的所有点通过此种变换变到
下方的所有点通过此种变换变到![]() 上方.由于四点不共圆,故
上方.由于四点不共圆,故![]() 上方的所有点对
上方的所有点对![]() 的张角大小互不相同.将除
的张角大小互不相同.将除![]() 外的
外的![]() 个点按张角从小到大的顺序标号
个点按张角从小到大的顺序标号![]() .若此点原来就在
.若此点原来就在![]() 上方,则标记“上”;若此点是由原来在
上方,则标记“上”;若此点是由原来在![]() 下方的点变换而得,则标“下”.由于每个点只和它对
下方的点变换而得,则标“下”.由于每个点只和它对![]() 的张角的大小有关系,故不妨将
的张角的大小有关系,故不妨将![]() 个点排成一条与
个点排成一条与![]() 垂直的直线
垂直的直线![]() ,张角小的在上.注意到,若过
,张角小的在上.注意到,若过![]() 、
、![]() 、
、![]() 三点作圆
三点作圆![]() ,则对于那些标有“下”的点来说,若它处于圆
,则对于那些标有“下”的点来说,若它处于圆![]() 内,则变换前必处于圆
内,则变换前必处于圆![]() 外,反之亦然.
外,反之亦然.
从而,过点![]() 、
、![]() 、
、![]() 的圆为好圆等价于
的圆为好圆等价于![]() 上方的“上”点数
上方的“上”点数![]() 下方的“下”点数
下方的“下”点数
![]() 下方的“上”点数
下方的“上”点数![]() 上方的“下”点数
上方的“下”点数![]() . ①
. ①
于是,只须证明:满足上面条件的![]() 有奇数个.
有奇数个.
(1)当![]() 均为“上”点,显然,只有一个点
均为“上”点,显然,只有一个点![]() 满足条件,点数为奇数.
满足条件,点数为奇数.
此时,“下”点个数为0个.
(2)若![]() ,易知点数为奇数.
,易知点数为奇数.
对一般的![]() 个点:
个点:
(i)若1和![]() 均标“上”,则1和
均标“上”,则1和![]() 必同时满足或不满足条件.
必同时满足或不满足条件.
而由对称性,可去掉1,![]() 两点,剩下的点原来满足条件与否等价于现在满足条件与否.
两点,剩下的点原来满足条件与否等价于现在满足条件与否.
故可把![]() 个点的情形化为
个点的情形化为![]() 个点的情形(它们的奇偶性相同).
个点的情形(它们的奇偶性相同).
(ii)若1,![]() 两点中有1个点标“下”,不妨设为1,把点1标的“下”改为“上”,并放到
两点中有1个点标“下”,不妨设为1,把点1标的“下”改为“上”,并放到![]() 点的下面,标号
点的下面,标号![]() ,则原来点1满足式①当且仅当现在点
,则原来点1满足式①当且仅当现在点![]() 满足式①,原来
满足式①,原来![]() 满足式①当且仅当现在变换后点
满足式①当且仅当现在变换后点![]() 满足式①.若是点
满足式①.若是点![]() 标“下”,把“下”改为“上”放到点1的上面,情况完全类似.此时,“下”的个数减少1,虽然点数没变.
标“下”,把“下”改为“上”放到点1的上面,情况完全类似.此时,“下”的个数减少1,虽然点数没变.
故不断对![]() 个点进行操作(i)或(ii),可使得点数不断减少(每次减少2)或“下”点数不断减少(每次减少1).于是,有限步后,必变成无标“下”的点或只有3个点的情形.此时,由(1)、(2)即可获证.
个点进行操作(i)或(ii),可使得点数不断减少(每次减少2)或“下”点数不断减少(每次减少1).于是,有限步后,必变成无标“下”的点或只有3个点的情形.此时,由(1)、(2)即可获证.
综上所述,原命题得证.


科目:高中数学 来源: 题型:
【题目】金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生.新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了160名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
(1)根据上表说明,能否有99%把握认为愿意参加新生接待工作与性别有关;
(2)现从参与问卷调查且愿意参加新生接待工作的学生中,采用按性别分层抽样的方法,选取10人.若从这10人中随机选取3人到火车站迎接新生,设选取的3人中女生人数为![]() ,写出
,写出![]() 的分布列,并求
的分布列,并求![]() .
.
附: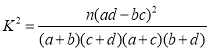 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 与直线
与直线![]() 相切且与圆
相切且与圆![]() 外切。
外切。
(1)求圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设第一象限内的点![]() 在轨迹
在轨迹![]() 上,若
上,若![]() 轴上两点
轴上两点![]() ,
,![]() ,满足
,满足![]() 且
且![]() . 延长
. 延长![]() 、
、![]() 分别交轨迹
分别交轨迹![]() 于
于![]() 、
、![]() 两点,若直线
两点,若直线![]() 的斜率
的斜率![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
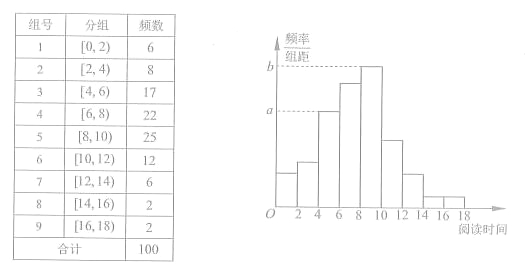
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年在印度尼西亚日惹举办的亚洲乒乓球锦标赛男子团体决赛中,中国队与韩国队相遇,中国队男子选手A,B,C,D,E依次出场比赛,在以往对战韩国选手的比赛中他们五人获胜的概率分别是0.8,0.8,0.8,0.75,0.7,并且比赛胜负相互独立.赛会釆用5局3胜制,先赢3局者获得胜利.
(1)在决赛中,中国队以3∶1获胜的概率是多少?
(2)求比赛局数的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com