
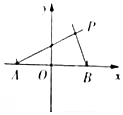
 如图,设A,B两点的坐标分别为(-$\sqrt{2}$,0),(${\sqrt{2}$,0).直线AP,BP相交于点P,且它们的斜率之积为-$\frac{1}{2}$.
如图,设A,B两点的坐标分别为(-$\sqrt{2}$,0),(${\sqrt{2}$,0).直线AP,BP相交于点P,且它们的斜率之积为-$\frac{1}{2}$.分析 (1)设点M的坐标为(x,y),求出斜率,列出方程化简求解即可.
(2)①若MN垂直于x轴,此时MN为椭圆的短轴,∴原点到直线MN的距离为0.
②若MN与x轴不垂直,设直线MN的方程为y=kx+b,原点O到直线MN的距离为h,由$\left\{\begin{array}{l}y=kx+b\\ \frac{x^2}{2}+{y^2}=1\end{array}\right.$,设M(x1,y1),N(x2,y2),利用韦达定理以及弦长公式,得到k与b的关系,然后求解距离的最大值.
解答 解:(1)设点M的坐标为(x,y),则${k_{AM}}=\frac{y}{{x+\sqrt{2}}}({x≠-\sqrt{2}}),{k_{BM}}=\frac{y}{{x-\sqrt{2}}}({x≠\sqrt{2}})$.
由已知有$\frac{y}{{x+\sqrt{2}}}•\frac{y}{{x-\sqrt{2}}}=-\frac{1}{2}({x≠±\sqrt{2}})$,化简得P的轨迹方程为$\frac{x^2}{2}+{y^2}=1({x≠±\sqrt{2}})$.
(2)①若MN垂直于x轴,此时MN为椭圆的短轴,∴原点到直线MN的距离为0.
②若MN与x轴不垂直,设直线MN的方程为y=kx+b,原点O到直线MN的距离为h,由$\left\{\begin{array}{l}y=kx+b\\ \frac{x^2}{2}+{y^2}=1\end{array}\right.$得:(1+2k2)x2+4kbx+2b2-2=0,∵△=16k2b2-8(1+2k2)(b2-1)>0,∴b2<2k2+1,…(*)
设M(x1,y1),N(x2,y2),则${x_1}+{x_2}=\frac{-4kb}{{1+2{k^2}}},{x_1}•{x_2}=\frac{{2({{b^2}-1})}}{{1+2{k^2}}}$.∵$|{MN}|=2,\sqrt{1+{k^2}}\sqrt{{{({{x_1}+{x_2}})}^2}-4{x_1}{x_2}}=2$,∴$({1+{k^2}})[{{{({-\frac{-4kb}{{1+2{k^2}}}})}^2}-\frac{{8({{b^2}-1})}}{{1+2{k^2}}}}]=4$,
整理得$\frac{1}{{1+{k^2}}}=2({1-{b^2}})$,∵1+k2≥1,∴$0<\frac{1}{{1+{k^2}}}≤1$,即0<2(1-b2)≤1,即$\frac{1}{2}≤{b^2}<1$,满足(*)式,∴$\frac{1}{2}≤{b^2}<1,{h^2}=\frac{b^2}{{1+{k^2}}}=2{b^2}({1-{b^2}})=2-{({{b^2}-\frac{1}{2}})^2}+\frac{1}{2}$,∴当${b^2}=\frac{1}{2}$时,h2取得最大值为$\frac{1}{2}$,
即h的最大值为$\frac{{\sqrt{2}}}{2}$.
点评 本题考查轨迹方程的求法,直线与椭圆的位置关系的应用,最值的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在四面体ABCD中,AD=1,CD=3,AC=2$\sqrt{3}$,cosB=$\frac{{\sqrt{3}}}{3}$.
如图所示,在四面体ABCD中,AD=1,CD=3,AC=2$\sqrt{3}$,cosB=$\frac{{\sqrt{3}}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 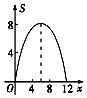 | B. | 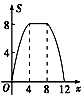 | C. |  | D. | 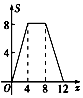 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com