
分析 (1)函数f(x)在x∈[1,2]上单调递减,在x∈[2,3]上单调递增,f(x)的最大值为max{f(1),f(3)};
(2)对原式化简换元有:设μ=2x+1,x∈[0,1],1≤μ≤3,则y=$μ+\frac{4}{μ}$-8,从而判断函数的单调性,利用集合的关系求出a范围.
解答 解:(1)由已知可以知道,函数f(x)在x∈[1,2]上单调递减,在x∈[2,3]上单调递增,
f(x)min=f(2)=2+2=4,又f(1)=1+4=5,f(3)=3+$\frac{4}{3}$=$\frac{13}{3}$;
f(1)>f(3)所以f(x)max=f(1)=5
所以f(x)在x∈[1,3]的值域为[4,5].
(2)y=g(x)=$\frac{4{x}^{2}-12x-3}{2x+1}$=2x+1+$\frac{4}{2x+1}$-8
设μ=2x+1,x∈[0,1],1≤μ≤3,则y=$μ+\frac{4}{μ}$-8,
由已知性质得,
当1≤u≤2,即0≤x≤$\frac{1}{2}$时,g(x)单调递减,所以递减区间为[0,$\frac{1}{2}$];
当2≤u≤3,即$\frac{1}{2}$≤x≤1时,g(x)单调递增,所以递增区间为[$\frac{1}{2}$,1];
由g(0)=-3,g($\frac{1}{2}$)=-4,g(1)=-$\frac{11}{3}$,得g(x)的值域为[-4,-3].
因为h(x)=-x-2a为减函数,故h(x)∈[-1-2a,-2a],x∈[0,1].
根据题意,g(x)的值域为h(x)的值域的子集,
从而有$\left\{\begin{array}{l}{-1-2a≤-4}\\{-2a≥-3}\end{array}\right.$,所以a=$\frac{3}{2}$.
点评 本题主要考查了函数的单调性,值域与集合关系以及对新定义理解,属中等题.


科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (0,1) | C. | $(0,\frac{1}{2})$ | D. | (-1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
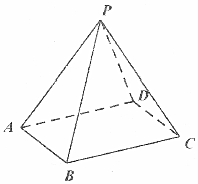 在底面是菱形的四棱锥P-ABCD中,∠BAD=60°,AB=2,PA=PC=2,PB=PD=$\sqrt{2}$.
在底面是菱形的四棱锥P-ABCD中,∠BAD=60°,AB=2,PA=PC=2,PB=PD=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (0,1) | C. | (0,$\frac{1}{2}$) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
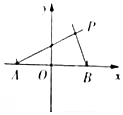 如图,设A,B两点的坐标分别为(-$\sqrt{2}$,0),(${\sqrt{2}$,0).直线AP,BP相交于点P,且它们的斜率之积为-$\frac{1}{2}$.
如图,设A,B两点的坐标分别为(-$\sqrt{2}$,0),(${\sqrt{2}$,0).直线AP,BP相交于点P,且它们的斜率之积为-$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com