
已知曲线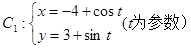 (t为参数),
(t为参数),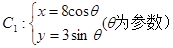
(1)化C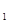 ,C
,C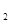 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C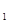 上的点P对应的参数为
上的点P对应的参数为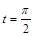 ,Q为C
,Q为C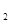 上的动点,求
上的动点,求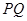 中点
中点 到直线
到直线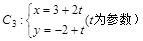 (t为参数)距离的最小值。
(t为参数)距离的最小值。
科目:高中数学 来源: 题型:解答题
(本小题10分)选修4—4:坐标系与参数方程
已知曲线C1的参数方程为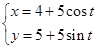 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ。
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ。
(Ⅰ)把C1的参数方程化为极坐标方程;
(Ⅱ)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在直角坐标系xOy中,直线l的参数方程为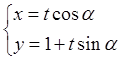 (t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ.
(t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ.
(1)求直线l与曲线C的平面直角坐标方程;
(2)设直线l与曲线C交于不同的两点A、B,若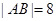 ,求α的值.
,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在直接坐标系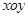 中,直线
中,直线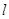 的方程为
的方程为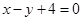 ,曲线
,曲线 的参数方程为
的参数方程为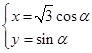 (
(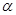 为参数)
为参数)
(I)已知在极坐标(与直角坐标系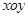 取相同的长度单位,且以原点
取相同的长度单位,且以原点 为极点,以
为极点,以 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点 的极坐标为(4,
的极坐标为(4,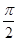 ),判断点
),判断点 与直线
与直线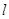 的位置关系;
的位置关系;
(II)设点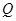 是曲线
是曲线 上的一个动点,求它到直线
上的一个动点,求它到直线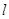 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某班有48名学生,在一次考试中统计出平均分为70分,方差为75,后来发现有2名同学的分数登错了,甲实得80分却记了50分,乙得70分却记了100分,更正后平均分和方差分别是( )
| A.70,75 | B.70,50 | C.70.1.04 | D.65,25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com