
【题目】已知过点![]() 且离心率为
且离心率为![]() 的椭圆
的椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上.
轴上.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆的左准线与
是椭圆的左准线与![]() 轴的交点,过点
轴的交点,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,记椭圆
两点,记椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,上下两个顶点分别为
,上下两个顶点分别为![]() .当线段
.当线段![]() 的中点落在四边形
的中点落在四边形![]() 内(包括边界)时,求直线
内(包括边界)时,求直线![]() 斜率的取值范围.
斜率的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
试题分析:(1)设椭圆的方程,用待定系数法求出![]() 的值;(2)解决直线和椭圆的综合问题时需注意:第一步,根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步,联立方程,把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步,求解判别式
的值;(2)解决直线和椭圆的综合问题时需注意:第一步,根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步,联立方程,把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步,求解判别式![]() ,计算一元二次方程根.第四步,根据题设条件求解问题中结论.
,计算一元二次方程根.第四步,根据题设条件求解问题中结论.
试题解析:(1)依题意,设椭圆![]() 的方程为
的方程为![]() (
(![]() ),焦距为
),焦距为![]() ,
,
由题设条件知,![]() ,即
,即![]() ,所以
,所以![]() ,由椭圆过点
,由椭圆过点![]() ,则有
,则有![]() ,解得
,解得![]() ,
,![]() ,故椭圆
,故椭圆![]() 的方程为
的方程为![]() .·······7分
.·······7分
(2)椭圆![]() 的左准线方程为
的左准线方程为![]() ,所以点
,所以点![]() 的坐标为(-4,0),
的坐标为(-4,0),
显然直线![]() 的斜率
的斜率![]() 存在,所以直线
存在,所以直线![]() 的方程为
的方程为![]() .
.
设点![]() 的坐标分别为
的坐标分别为![]() ,线段
,线段![]() 的
的
中点为![]() ,
,
由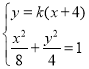
得![]() , ① ·······9分
, ① ·······9分
由![]() ,
,
解得![]() , ② ·······11分
, ② ·······11分
因为![]() 是方程①的两根,所以
是方程①的两根,所以![]() ,
,
于是![]() ,
,![]() ·······12分
·······12分
∵![]() ,所以点
,所以点![]() 不可能在
不可能在![]() 轴的右边.
轴的右边.
又直线![]() 方程分别为
方程分别为![]() ,
,![]()
所以点![]() 在正方形
在正方形![]() 内(包括边界)的充要条件为
内(包括边界)的充要条件为
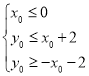 ,即
,即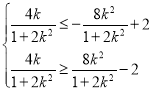 ·······14分
·······14分
解得![]() ,此时②也成立.故直线
,此时②也成立.故直线![]() 斜率的取值范围是
斜率的取值范围是![]() . ······16分
. ······16分


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】某食品厂定期购买面粉.已知该厂每天需用面粉6t,每吨面粉的价格为1800元,面粉的保管等其他费用为平均每吨每天3元,购面粉每次需支付运费900元.
(1)求该厂多少天购买一次面粉,才能使平均每天所支付的总费用最少?
(2)若提供面粉的公司规定:当一次购买面粉不少于210t时,其价格可享受9折优惠(即原价的90%),问该厂是否考虑利用此优惠条件?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1.
(Ⅰ)求数列{an}的通项公式.
(Ⅱ)设数列{bn}的前n项和为Tn,且Tn+![]() =λ(λ为常数),令cn=b2n(n∈N*).求数列{cn}的前n项和Rn.
=λ(λ为常数),令cn=b2n(n∈N*).求数列{cn}的前n项和Rn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线
轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知直线![]() 的参数方程是
的参数方程是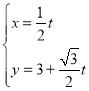 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,点
两点,点![]() 为
为![]() 的中点,点
的中点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣1,g(x)=﹣x2+4x﹣3,若有f(a)=g(b),则b的取值范围为( )
A.![]()
B.(2﹣ ![]() ,2+
,2+ ![]() )
)
C.[1,3]
D.(1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,过点
,过点![]() 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,
, ![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,连接
两点,连接![]() (
(![]() 为坐标原点)并延长交椭圆
为坐标原点)并延长交椭圆![]() 于点
于点![]() ,求
,求![]() 面积的最大值及取最大值时直线
面积的最大值及取最大值时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 内,动点
内,动点![]() 与两定点
与两定点![]() ,
, ![]() 连线的斜率之积为
连线的斜率之积为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设点![]() ,
, ![]() 是轨迹
是轨迹![]() 上相异的两点.
上相异的两点.
(Ⅰ)过点![]() ,
, ![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() ,
, ![]() ,
, ![]() 与
与![]() 两条切线相交于点
两条切线相交于点![]() ,证明:
,证明: ![]() ;
;
(Ⅱ)若直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,证明:
,证明: ![]() 为定值,并求出这个定值.
为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=2,点E、F分别在边AB、DC上,M为AD的中点,且 ![]() =0,则△MEF的面积的取值范围为( )
=0,则△MEF的面积的取值范围为( ) 
A.![]()
B.[1,2]
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com