
分析 由条件利用二倍角的正切公式,即可解得tanα的值,进而可求tan2α的值.
解答 解:∵tan$\frac{α}{2}$=2,
∴tanα=$\frac{2tan\frac{α}{2}}{1-ta{n}^{2}\frac{α}{2}}$=$\frac{2×2}{1-{2}^{2}}$=-$\frac{4}{3}$,
tan2α=$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{2×(-\frac{4}{3})}{1-(-\frac{4}{3})^{2}}$=$\frac{24}{7}$.
故答案为:$\frac{24}{7}$.
点评 本题主要考查二倍角的正切公式的应用,考查了计算能力,属于基础题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$-1 | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东清远三中高二上学期第一次月考数学(理)试卷(解析版) 题型:选择题
已知圆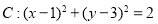 被直线
被直线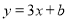 所截得的线段的长度等于2,则
所截得的线段的长度等于2,则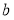 等于( )
等于( )
A.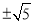 B.
B.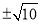 C.
C.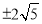 D.
D.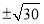
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
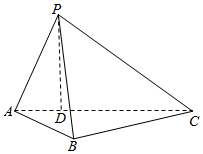 如图所示,在三棱锥P-ABC中,$AB=BC=2\sqrt{3}$,平面PAC⊥平面ABC,PD⊥AC于点D,AD=2,CD=4,PD=3.
如图所示,在三棱锥P-ABC中,$AB=BC=2\sqrt{3}$,平面PAC⊥平面ABC,PD⊥AC于点D,AD=2,CD=4,PD=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $m≥\frac{1}{4}$或m=-1 | B. | $m≥\frac{1}{4}$ | C. | $m≥\frac{1}{5}$或m=-1 | D. | $m≥\frac{1}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com