练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知等差数列{an}的前n项和为Sn，若a2＝3，a6＝11，则S7＝

        A．91           B．          C．98           D．49


    D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    是否存在常数a, b使等式对于一切n∈N*都成立？若存在，求出a, b的值，若不存在，请说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知tan(＋α)＝.

    （1）求tanα的值；

    （2）求的值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    给出下列四个命题：①函数y＝2cos2(x＋)的图像可由曲线y＝1＋cos2x向左平移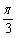个单位得到；②函数y＝sin(x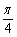＋)＋cos(x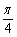＋)是偶函数；③直线x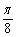＝是曲线y＝sin(2x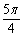＋)的一条对称轴；④函数y＝2sin2(x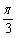＋)的最小正周期是2π.

    其中不正确命题的序号是                  。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


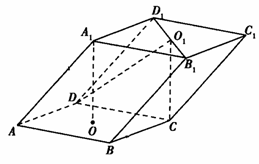
    如图，已知平行六面体ABCD—A1B1C1D1的底面为正方形，O1、O分别为上、下底面的中心，且A1在底面ABCD上的射影是O。

    （1）求证：平面O1DC⊥平面ABCD；

    （2）若∠A1AB＝60°，求平面BAA1与平面CAA1的夹角的余弦值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝sin(wx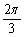＋)＋sin(wx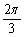－)(w＞0)的最小正周期为π，则

        A．f(x)在(0, 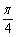)上单调递增      B．f(x)在(0, 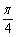)上单调递减

        C．f(x)在(0, )上单调递增      D．f(x)在(0, )上单调递减

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    定义在R上的函数f(x)及其导函数f ' (x)的图像都是连续不断的曲线，且对于实数a, b (a＜b)有f ' (a)＞0, f ' (b)＜0，现给出如下结论：

    ①$x0∈[a, b], f(x0)＝0；②$x0∈[a, b], f(x0)＞f(b)；

    ③"x0∈[a, b], f(x0)＞f(a)；④$x0∈[a, b], f(a)－f(b)＞f ' (x0)(a－b).

    其中结论正确的有                。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


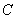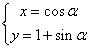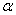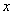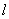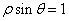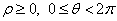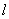    （1）已知圆的参数方程为（为参数），以原点为极点，轴正半轴为极轴建立极坐标系，直线的极坐标方程为,()则直线与圆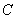的交点的极坐标为______________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     函数在区间上的最大值为,则实数的值为(    )

    A．  或       B．        C．       D． 或

    查看答案和解析>>

    同步练习册答案