
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 的值及
的值及![]() 的单调区间;
的单调区间;
(2)当![]() 时,求证:
时,求证:![]() 在定义域内有且只有两个极值点.
在定义域内有且只有两个极值点.
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,已知点A(5,-2),B(7,3),且边AC的中点M在y轴上,边BC的中点N在x轴上,求:
(1)顶点C的坐标;
(2)直线MN的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P不在直线l、m上,则“过点P可以作无数个平面,使得直线l、m都与这些平面平行”是“直线l、m互相平行”的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若不经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,且直线
,且直线![]() 与直线
与直线![]() 的斜率之和为1,试判断直线
的斜率之和为1,试判断直线![]() 是否过定点.若过定点,请求出该定点;若不过定点,请说明理由.
是否过定点.若过定点,请求出该定点;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着互联网的发展,诸如“滴滴打车”“神州专车”等网约车服务在我国各:城市迅猛发展,为人们出行提供了便利,但也给城市交通管理带来了一些困难.为掌握网约车在![]() 省的发展情况,
省的发展情况,![]() 省某调查机构从该省抽取了
省某调查机构从该省抽取了![]() 个城市,分别收集和分析了网约车的
个城市,分别收集和分析了网约车的![]() 两项指标数
两项指标数![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
|
|
|
|
|
|
|
|
|
|
|
|
经计算得: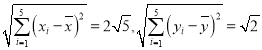
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并利用
,并利用![]() 说明
说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标数为
指标数为![]() 时,
时,![]() 指标数的估计值.
指标数的估计值.
附:相关公式: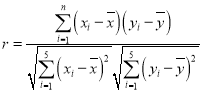 ,
,
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若直线![]() 与曲线
与曲线![]() 满足以下两个条件:点
满足以下两个条件:点![]() 在曲线
在曲线![]() 上,直线
上,直线![]() 方程为
方程为![]() ;曲线
;曲线![]() 在点
在点![]() 附近位于直线
附近位于直线![]() 的两侧,则称直线
的两侧,则称直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]() .下列选项正确的是( )
.下列选项正确的是( )
A.直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]()
B.直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]()
C.直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]()
D.直线![]() 在点
在点![]() 处“切过”曲线
处“切过”曲线![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省积极响应教育部号召实行新课程改革,为了调查某校高三学生的物理考试成绩是否达到![]() 级与学生性别是否有关,从该校高三学生中随机抽取了部分男女生的成绩得到如下列联表:
级与学生性别是否有关,从该校高三学生中随机抽取了部分男女生的成绩得到如下列联表:
考试成绩达到 | 考试成绩未达到 | 总计 | |
男生 | 26 | 40 | |
女生 | 6 | ||
总计 | 70 |
(1)(ⅰ)将![]() 列联表补充完整;
列联表补充完整;
(ⅱ)据此列联表判断,能否有![]() 的把握认为“物理考试成绩是否达到级与性别有关”?
的把握认为“物理考试成绩是否达到级与性别有关”?
(2)将频率视作概率,从该校高三年级任意抽取3名学生的成绩,求物理考试成绩达到![]() 级的人数的分布列及期望.
级的人数的分布列及期望.
附: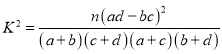
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10..828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com