
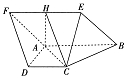
 如图,菱形ABEF所在平面与直角梯形ABCD所在的平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.
如图,菱形ABEF所在平面与直角梯形ABCD所在的平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.分析 (1)由∠BAD=∠CDA=90°,可得AB∥CD,再由四边形ABEF为菱形,可得AB∥EF,得到EF∥CD.结合H是EF的中点,AB=2CD,得CD=FH,可得四边形CDFH为平行四边形,从而得到DF∥CH.再由线面平行的判定可得FD∥平面AHC;
(2)由平面ABEF⊥平面ABCD,DA⊥AB,可得DA⊥平面ABEF,结合已知可得四棱锥C-ABEF的高DA=2,三棱锥F-ADC的高AH=$\sqrt{3}$.然后由VABCDEF=VC-ABEF+VF-ADC求得多面体ABCDEF的体积.
解答 (1)证明:∵∠BAD=∠CDA=90°,∴AB∥CD,
∵四边形ABEF为菱形,∴AB∥EF,则EF∥CD.
∵H是EF的中点,AB=2CD,∴CD=FH,
∴四边形CDFH为平行四边形,则DF∥CH.
∵DF?平面AHC,HC?平面AHC,
∴FD∥平面AHC;
(2)解:∵平面ABEF⊥平面ABCD,DA⊥AB,
∴DA⊥平面ABEF,
∵DC∥AB,∴四棱锥C-ABEF的高DA=2,
∵∠ABE=60°,四边形ABEF为边长是4的菱形,
∴可求三棱锥F-ADC的高AH=2$\sqrt{3}$.
∴VABCDEF=VC-ABEF+VF-ADC=$\frac{1}{3}×4×2\sqrt{3}×2+\frac{1}{3}×\frac{1}{2}×2×2×2\sqrt{3}$=$\frac{20\sqrt{3}}{3}$.
点评 本题考查线面平行的判定,考查了空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分数 | [85,100] | [70,85) | [60,70) | [0,60) |
| 等级 | A等 | B等 | C等 | D等 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | χ2≥3.841 | B. | χ2≤3.841 | C. | χ2≥6.635 | D. | χ2≤6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\sqrt{3})$ | B. | $(\sqrt{2},\sqrt{3})$ | C. | $(\sqrt{2},2)$ | D. | $(\sqrt{3},2)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {-1,1} | C. | {-1,1,2} | D. | {0,1,2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com