
| A. | $(1,\sqrt{3})$ | B. | $(\sqrt{2},\sqrt{3})$ | C. | $(\sqrt{2},2)$ | D. | $(\sqrt{3},2)$ |
分析 由条件可得$\frac{π}{2}$<3 A<π,且 0<2A<$\frac{π}{2}$,故 $\frac{π}{6}$<A<$\frac{π}{4}$,$\frac{\sqrt{2}}{2}$<cosA<$\frac{\sqrt{3}}{2}$,由正弦定理可得 b=2cosA,从而得到 b 的取值范围.
解答 解:在锐角△ABC中,a=1,∠B=2∠A,
∴$\frac{π}{2}$<3 A<π,且 0<2A<$\frac{π}{2}$,故 $\frac{π}{6}$<A<$\frac{π}{4}$,
故 $\frac{\sqrt{2}}{2}$<cosA<$\frac{\sqrt{3}}{2}$.
由正弦定理可得 $\frac{1}{sinA}=\frac{b}{sin2A}$=$\frac{b}{2sinAcosA}$,
∴b=2cosA,
∴$\sqrt{2}$<b<$\sqrt{3}$,
故选:B.
点评 本题考查锐角三角形的定义,正弦定理的应用,求得 $\frac{π}{6}$<A<$\frac{π}{4}$,是解题的关键,属于中档题.


 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
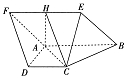 如图,菱形ABEF所在平面与直角梯形ABCD所在的平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.
如图,菱形ABEF所在平面与直角梯形ABCD所在的平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12,-15 | B. | 5,-15 | C. | 12,-5 | D. | 5,-16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,为了研究某城市2016年的空气质量情况,省环保局从全年的检测数据中随机抽取了30天进行统计,得到茎叶图如图所示,则该样本的中位数、众数、极差分别是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,为了研究某城市2016年的空气质量情况,省环保局从全年的检测数据中随机抽取了30天进行统计,得到茎叶图如图所示,则该样本的中位数、众数、极差分别是( )| A. | 76,75,56 | B. | 76,75,53 | C. | 77,75,56 | D. | 75,77,53 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{2}}{8}$ | C. | $\frac{\sqrt{2}}{12}$ | D. | $\frac{\sqrt{2}}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com