
分析 (1)求导数,利用f′(x)=a-cosx≥0在R上恒成立,求实数a的取值范围;
(2)当a=$\frac{1}{2}$时,求导数,确定函数的单调性,即可求函数f(x)在区间[0,$\frac{π}{2}$]上的最大值与最小值.
解答 解:(1)∵f(x)=ax-sinx,
∴f′(x)=a-cosx,
∵函数f(x)在R上是单调增函数,
∴f′(x)=a-cosx≥0在R上恒成立,
∴a≥1;
(2)当a=$\frac{1}{2}$时,f′(x)=$\frac{1}{2}$-cosx,
∴当x∈($\frac{1}{3}π$,$\frac{1}{2}$π)时,f'(x)>0,f(x)递增
当x∈(0,$\frac{1}{3}π$)时,f'(x)<0,f(x)递减
∴f(x)的最大值为f(0)=$\frac{π}{4}$-1,f(x)的最小值为f($\frac{1}{3}π$)=$\frac{π}{6}$-$\frac{\sqrt{3}}{2}$,
点评 本题考查导数知识的综合运用,考查函数的单调性、最值,考查学生分析解决问题的能力,属于中档题.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知D是△ABC边BC上一点.
如图,已知D是△ABC边BC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | $8+\sqrt{13}$ | C. | 4 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{8\sqrt{2}}}{3}π$ | B. | $\frac{{4\sqrt{2}}}{3}π$ | C. | $\frac{4}{3}π$ | D. | $\frac{32}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
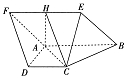 如图,菱形ABEF所在平面与直角梯形ABCD所在的平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.
如图,菱形ABEF所在平面与直角梯形ABCD所在的平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,为了研究某城市2016年的空气质量情况,省环保局从全年的检测数据中随机抽取了30天进行统计,得到茎叶图如图所示,则该样本的中位数、众数、极差分别是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,为了研究某城市2016年的空气质量情况,省环保局从全年的检测数据中随机抽取了30天进行统计,得到茎叶图如图所示,则该样本的中位数、众数、极差分别是( )| A. | 76,75,56 | B. | 76,75,53 | C. | 77,75,56 | D. | 75,77,53 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com