
分析 设∠DBM=θ,在△CDA中,由正弦定理可得$\frac{CD}{sin(\frac{π}{2}-2θ)}$=$\frac{AC}{sin2θ}$,在△AMB中,由正弦定理可得$\frac{MA}{sin(\frac{π}{2}-2θ)}$=$\frac{AB}{sin(π-θ)}$,继而可得$\frac{CD}{MA}$=$\frac{1}{2}$,问题得以解决
解答  解:设∠DBM=θ,则∠ADC=2θ,∠DAC=$\frac{π}{2}$-2θ,∠AMB=$\frac{π}{2}$-2θ,
解:设∠DBM=θ,则∠ADC=2θ,∠DAC=$\frac{π}{2}$-2θ,∠AMB=$\frac{π}{2}$-2θ,
在△CDA中,由正弦定理可得$\frac{CD}{sin(\frac{π}{2}-2θ)}$=$\frac{AC}{sin2θ}$,
在△AMB中,由正弦定理可得$\frac{MA}{sin(\frac{π}{2}-2θ)}$=$\frac{AB}{sin(π-θ)}$,
∴$\frac{CD}{MA}$=$\frac{ACsinθ}{ABsin2θ}$=$\frac{ACsinθ}{2ABsinθcosθ}$=$\frac{1}{2}$,
从而MA=2,
故答案为:2.
点评 本题考查了正弦定理的应用,关键是掌握应用的条件,属于中档题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{8\sqrt{2}}}{3}π$ | B. | $\frac{{4\sqrt{2}}}{3}π$ | C. | $\frac{4}{3}π$ | D. | $\frac{32}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{7}{6}$,+∞) | B. | (-∞,$\frac{7}{6}$) | C. | (-∞,$\frac{1}{3}$) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
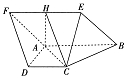 如图,菱形ABEF所在平面与直角梯形ABCD所在的平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.
如图,菱形ABEF所在平面与直角梯形ABCD所在的平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H是线段EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12,-15 | B. | 5,-15 | C. | 12,-5 | D. | 5,-16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{4}$ | B. | $\frac{\sqrt{2}}{8}$ | C. | $\frac{\sqrt{2}}{12}$ | D. | $\frac{\sqrt{2}}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com