
【题目】已知椭圆C以坐标轴为对称轴,以坐标原点为对称中心,椭圆的一个焦点为![]() ,点
,点![]() 在椭圆上,
在椭圆上,
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程.
求椭圆C的方程.
![]() Ⅱ
Ⅱ![]() 斜率为k的直线l过点F且不与坐标轴垂直,直线l交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
斜率为k的直线l过点F且不与坐标轴垂直,直线l交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
【答案】![]() Ⅰ
Ⅰ![]()
![]() .
.![]() Ⅱ
Ⅱ![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 设椭圆方程为
设椭圆方程为![]() ,由椭圆可得
,由椭圆可得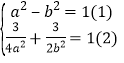 ,解出即可得出.
,解出即可得出.
![]() Ⅱ
Ⅱ![]() 解法一:设
解法一:设![]() ,
,![]() ,AB中点
,AB中点![]() ,直线AB的方程为
,直线AB的方程为![]() ,代入椭圆方程可得
,代入椭圆方程可得![]() ,利用根与系数的关系、中点坐标公式可得N的坐标,可得AB的垂直平分线NG的方程为,进而得出.
,利用根与系数的关系、中点坐标公式可得N的坐标,可得AB的垂直平分线NG的方程为,进而得出.
解法二:设![]() ,
,![]() ,AB中点
,AB中点![]() ,把点A,B的坐标分别代入椭圆方程相减可得:
,把点A,B的坐标分别代入椭圆方程相减可得:![]() ,利用中点坐标公式、斜率计算公式可得斜率
,利用中点坐标公式、斜率计算公式可得斜率![]() ,又
,又![]() ,可得
,可得![]() ,又
,又![]() 在椭圆内,即
在椭圆内,即![]() ,可得
,可得![]() ,利用AB的垂直平分线为
,利用AB的垂直平分线为![]() ,即可得出.
,即可得出.
![]() Ⅰ
Ⅰ![]() 设椭圆方程为
设椭圆方程为![]() ,
,
则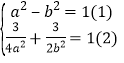
由![]() 得
得![]()
由![]() 得
得![]() 代入
代入![]() 得
得![]() ,
,
即![]() ,即
,即![]() ,或
,或![]()
![]() ,
,![]() ,得
,得![]() ,
,
![]() ,
,![]() ,
,
![]() 椭圆方程为
椭圆方程为![]() .
.
![]() Ⅱ
Ⅱ![]() 解法一:设
解法一:设![]() ,
,![]() ,AB中点
,AB中点![]() ,
,
直线AB的方程为![]() ,
,
代入![]() ,整理得
,整理得![]() ,
,
![]() 直线AB过椭圆的左焦点F,
直线AB过椭圆的左焦点F,![]() 方程有两个不等实根,
方程有两个不等实根,
则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 的垂直平分线NG的方程为
的垂直平分线NG的方程为![]() ,
,
![]() 时,
时,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
解法二:设![]() ,
,![]() ,AB中点
,AB中点![]() ,
,
由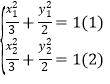 ,
,![]() 得
得![]() ,
,
斜率![]() ,
,
又![]() ,
,![]() ,
,
![]() ,得
,得![]() ,
,
![]() 在椭圆内,即
在椭圆内,即![]() ,
,
将![]() 代入得
代入得![]() ,
,
解得![]()
![]() ,
,
则AB的垂直平分线为![]() ,
,![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】从装有两个红球和两个黑球的口袋内任取两个球,那么互斥而不对立的两个事件是( )
A. “至少有一个黑球”与“都是红球”
B. “至少有一个黑球”与“至少有一个红球”
C. “至少有一个黑球”与“都是黑球”
D. “恰有一个黑球”与“恰有两个黑球”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某学校进行的一次语文与历史成绩中,随机抽取了25位考生的成绩进行分析,25位考生的语文成绩已经统计在茎叶图中,历史成绩如下:
(Ⅰ)请根据数据在茎叶图中完成历史成绩统计;
(Ⅱ)请根据数据完成语文成绩的频数分布表及语文成绩的频率分布直方图;
语文成绩的频数分布表:
语文成绩分组 | [50,60) | [60,70) | [70,80) | [90,100) | [100,110) | [110,120] |
频数 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 上一点
上一点![]() 与椭圆右焦点的连线垂直于x轴,直线l:y=kx+m与椭圆C相交于A,B两点(均不在坐标轴上).
与椭圆右焦点的连线垂直于x轴,直线l:y=kx+m与椭圆C相交于A,B两点(均不在坐标轴上).
(1)求椭圆C的标准方程;
(2)设O为坐标原点,若△AOB的面积为![]() ,试判断直线OA与OB的斜率之积是否为定值?若是请求出,若不是请说明理由.
,试判断直线OA与OB的斜率之积是否为定值?若是请求出,若不是请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:![]() 经过点
经过点![]() ,与x轴正半轴交于点B.
,与x轴正半轴交于点B.
![]() Ⅰ
Ⅰ![]() ______;
______;![]() 将结果直接填写在答题卡的相应位置上
将结果直接填写在答题卡的相应位置上![]()
![]() Ⅱ
Ⅱ![]() 圆O上是否存在点P,使得
圆O上是否存在点P,使得![]() 的面积为15?若存在,求出点P的坐标;若不存在,说明理由.
的面积为15?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=2x2+(x﹣2a)|x﹣a|在区间[﹣3,1]上不是单调函数,则实数a的取值范围是( )
A.[﹣4,1]
B.[﹣3,1]
C.(﹣6,2)
D.(﹣6,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x0∈[0,2],log2(x+2)<2m;命题q:关于x的方程3x2﹣2x+m2=0有两个相异实数根.
(1)若(¬p)∧q为真命题,求实数m的取值范围;
(2)若p∨q为真命题,p∧q为假命题,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com